Advertisements (Quảng cáo)
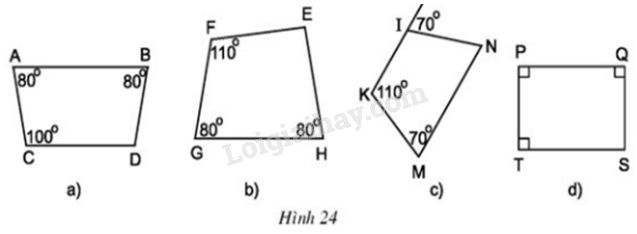
Cho hình \(24.\)
a) Tìm các hình thang cân.
b) Tính các góc còn lại của mỗi hình thang cân đó.
c) Có nhận xét gì về hai góc đối của hình thang cân?
Áp dụng:
+) Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
+) Định lí tổng các góc của một tứ giác.
+) Hai góc kề bù có tổng số đo bằng \(180^o\).
a) Các hình thang cân là: \(ABDC, IKMN, PQST\)
b)
Advertisements (Quảng cáo)
+) Hình thang cân \(ABCD\)
Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(ABCD\) ta có:
\(\eqalign{
& \widehat D = {360^o} – \left( {\widehat A + \widehat B + \widehat C} \right) \cr
& \,\,\,\,\,\, \;= {360^o} – \left( {{{80}^o} + {{80}^o} + {{100}^o}} \right) \cr
& \,\,\,\,\,\, \;= {360^o} – {260^o} = {100^o} \cr} \)
+) Hình thang cân \(IKMN\)
\(\widehat I = {180^o} – {70^o}\) (hai góc kề bù)
\(\Rightarrow \widehat I = {110^o}\)
\(\widehat N = {70^o}\) (hai góc so le trong)
+) Hình thang cân \(PQST\)
Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(PQST\) ta có:
\(\eqalign{
& \widehat S = {360^o} – \left( {\widehat P + \widehat Q + \widehat T} \right) \cr
& \,\,\,\,\, = {360^o} – \left( {{{90}^o} + {{90}^o} + {{90}^o}} \right) \cr
& \,\,\,\,\, = {360^o} – {270^o} = {90^o} \cr} \)
c) Hai góc đối của hình thang cân bù nhau.