Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.. Câu 25 trang 83 Sách bài tập (SBT) Toán 8 tập 1 - Bài 3. Hình thang cân
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
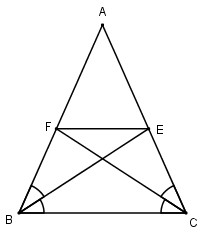
Xét hai tam giác AEB và AFC
Có AB = AC (∆ ABC cân tại A)
Advertisements (Quảng cáo)
\(\widehat {ABE} = {{\widehat B} \over 2} = {{\widehat C} \over 2} = \widehat {ACF}\) và \(\widehat A\) là góc chung
\( \Rightarrow \Delta ADB = \Delta AEC\left( {g.c.g} \right) \Rightarrow AE = AF \Rightarrow \Delta AEF\) cân tại A
\( \Rightarrow \widehat {AFE} = {{{{180}^0} - \widehat A} \over 2}\) và trong tam giác \(\Delta ABC:\,\,\widehat B = {{{{180}^0} - \widehat A} \over 2}\)
\( \Rightarrow \widehat {AFE} = \widehat B \Rightarrow FE//BC\) ⟹ tứ giác BFEC là hình thang.