. Câu 38 trang 162 Sách bài tập (SBT) Toán 8 tập 1 - Bài 4. Diện tích hình thang
Diện tích hình bình hành bằng 24\(c{m^2}\). Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng 2cm và 3cm. Tính chu vi của hình bình hành đó.
Giải:
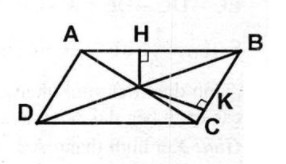
Gọi O là giao điểm hai đường chéo hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm, đến cạnh BC là OK = 3cm.
Kéo dài OH cắt cạnh CD tại H’
OH ⊥ AB ⇒ OH’ ⊥ CD và OH’ = 2cm
Advertisements (Quảng cáo)
nên HH’ bằng đường cao của hình bình hành
\(\eqalign{ & {S_{ABCD}} = HH’.AB \cr & \Rightarrow AB = {{{S_{ABCD}}} \over {HH’}} = {{24} \over 4} = 6(cm) \cr} \)
Kéo dài OK cắt AD tại K’
OK ⊥ BC ⇒ OK’ ⊥ AD và OK’ = 3 (cm)
nên KK’ là đường cao của hình bình hành
\({S_{ABCD}} = KK’.BC \Rightarrow BC = {{{S_{ABCD}}} \over {KK’}} = {{24} \over 6} = 4\) (cm)
Chu vi hình bình hành ABCD là (6 + 4) . 2 = 20 (cm)
