Một hình chữ nhật có các kích thước a và b. Một hình bình hành cùng có hai cạnh là a và b. Tính góc nhọn của hình bình hành nếu diện tích của nó bằng một nửa diện tích của hình chữ nhật (a và b có cùng đơn vị đo)
Giải:
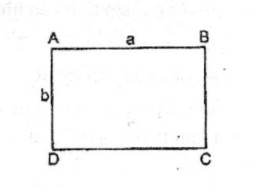
Xét hình chữ nhật ABCD có chiều dài AB = a, chiều rộng AD = b.
\( \Rightarrow {S_{ABCD}} = ab\)
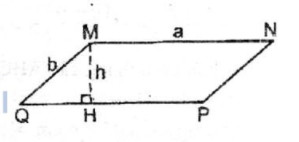
Hình bình hành MNPQ có góc M là góc tù, MN = a, cạnh MQ = b
Kẻ đường cao MH
Advertisements (Quảng cáo)
\({S_{MNPQ}} = MH.a\)
Theo bài ra ta có : \(MH.a = {1 \over 2}a.b\)
\( \Rightarrow MH = {1 \over 2}b$hay $MH = {{MQ} \over 2}\)
∆ MHQ vuông tại H và \(MH = {{MQ} \over 2}\)
Cạnh đối diện góc nhọn bằng một nửa cạnh huyền nên \(\widehat {MQH} = 30^\circ \)
Vậy góc nhọn của hình bình hành bằng \(30^\circ \)
