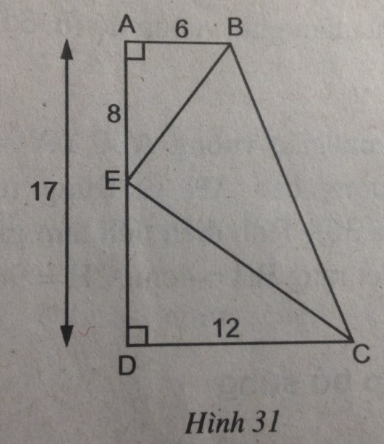
Cho hình thang vuông ABCD (\(\widehat A = \widehat D = 90^\circ \)) AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn thẳng AE = 8cm (h.31). Chứng minh góc BEC = 90°
Giải:
(hình 31 trang 95 sbt)
Ta có: AD = AE + DE
Suy ra: DE = AD – AE
=17 – 8 = 9 (cm)
Xét ∆ ABE và ∆ DEC, ta có:
\(\widehat A = \widehat D = 90^\circ \) (1)
Advertisements (Quảng cáo)
Mà \({{AB} \over {DE}} = {6 \over 9} = {2 \over 3}\)
\({{AE} \over {DC}} = {8 \over {12}} = {2 \over 3}\)
Suy ra: \({{AB} \over {DE}} = {{AE} \over {DC}}\) (2)
Từ (1) và (2) suy ra ∆ DEC đồng dạng ∆ ABE (c.g.c)
Suy ra: \(\widehat {AEB} = \widehat {DEC}\)
Trong ∆ ABE ta có: \(\widehat A = 90^\circ \Rightarrow \widehat {ABE} + \widehat {AEB} = 90^\circ \)
Suy ra: \(\widehat {DEC} + \widehat {AEB} = 90^\circ \)
Lại có: \(\widehat {ABE} + \widehat {BEC} + \widehat {DEC} = \widehat {AED} = 180^\circ \) (kề bù)
Vậy \(\widehat {BEC} = 180^\circ - \left( {\widehat {AEB} + \widehat {DEC}} \right) = 180^\circ - 90^\circ = 90^\circ \)
