Tam giác ABC vuông tại A có đường cao AH = n = 10,85cm và cạnh AB = m = 12,5cm. Hãy tính độ dài các cạnh còn lại của tam giác (chính xác đến hai chữ số thập phân)
Giải:
(hình bs. 13 trang 125 sbt)
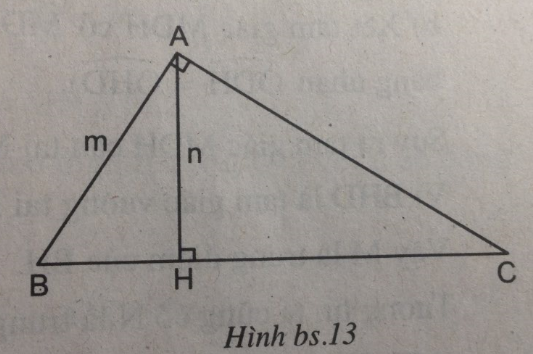
Xét hai tam giác ABC và HBA, ta có:
\(\widehat {BAC} = \widehat {BHA} = 1v\)
Góc B là góc nhọn chung
Advertisements (Quảng cáo)
Vậy ∆ ABC đồng dạng ∆ HBA
Suy ra: \(\eqalign{ & {{AB} \over {HB}} = {{AC} \over {HA}} = {{BC} \over {BA}} \cr & \Rightarrow {m \over {HB}} = {{AC} \over n} = {{BC} \over m} \cr & \Rightarrow AC = {{mn} \over {HB}},BC = {{{m^2}} \over {HB}}. \cr} \)
Xét tam giác vuông ABH, ta có:
\(HB = \sqrt {A{B^2} - A{H^2}} = \sqrt {{m^2} - {n^2}} \)
Từ đó, ta có: \(AC = {{m.n} \over {\sqrt {{m^2} - {n^2}} }};BC = {{{m^2}} \over {\sqrt {{m^2} - {n^2}} }}\)
Với m = 12,5cm, n = 10,85cm, ta tính được:
AC ≈ 21,85cm; BC ≈ 25,17cm.
