Chứng minh rằng. Câu 48 trang 95 Sách bài tập (SBT) Toán 8 tập 2 - Bài 8. Các trường hợp đồng dạng của tam giác vuông
Cho tam giác ABC (\(\widehat A = 90^\circ \)) có đường cao AH (h.34)
Chứng minh rằng \(A{H^2} = BH.CH\)
Giải:
(hình 34 trang 95 sbt)
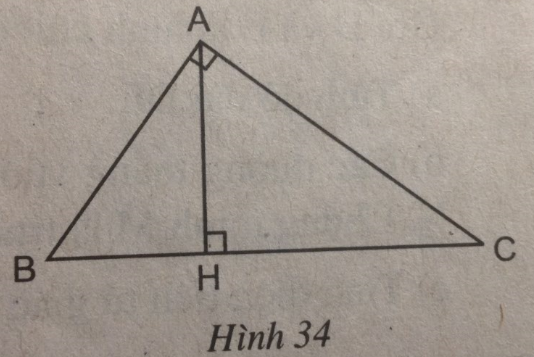
Xét hai tam giác vuông HBA và HAC, ta có:
Advertisements (Quảng cáo)
\(\widehat {HBA} = \widehat {AHC} = 90^\circ \)
\(\widehat B = \widehat {HAC}\) (hai góc cùng phụ góc C)
Suy ra: ∆ HBA đồng dạng ∆ HAC (g.g)
Suy ra: \({{HA} \over {HB}} = {{HC} \over {HA}}\)
Vậy \(A{H^2} = HB.HC\)
