Chứng minh rằng BD // AC.. Câu 46 trang 95 Sách bài tập (SBT) Toán 8 tập 2 - Bài 8. Các trường hợp đồng dạng của tam giác vuông
Cho tam giác ABC vuông tại A, AC = 4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC).Lấy trên tia Cx điểm D sao cho BD = 9cm (h.32)
Chứng minh rằng BD // AC.
Giải:
(hình 32 trang 95 sbt)
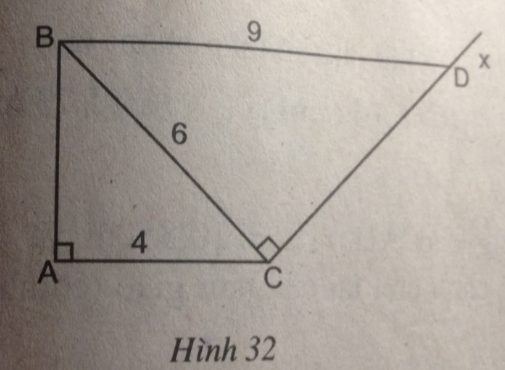
Xét hai tam giác vuông ABC và CDB, ta có:
\(\widehat {BAC} = \widehat {DCB} = 90^\circ \) (1)
Advertisements (Quảng cáo)
Mà \({{AC} \over {CB}} = {4 \over 6} = {2 \over 3}\)
\({{CB} \over {BD}} = {6 \over 9} = {2 \over 3}\)
Suy ra: \({{AC} \over {CB}} = {{CB} \over {BD}}\) (2)
Từ (1) và (2) suy ra ∆ ABC đồng dạng ∆ CDB (cạnh huyền và cạnh góc vuông tỉ lệ)
Suy ra: \(\widehat {ACB} = \widehat {CBD}\)
Vậy AC // BD (vì có các cặp góc ở vị trí so le trong bằng nhau).