Advertisements (Quảng cáo)
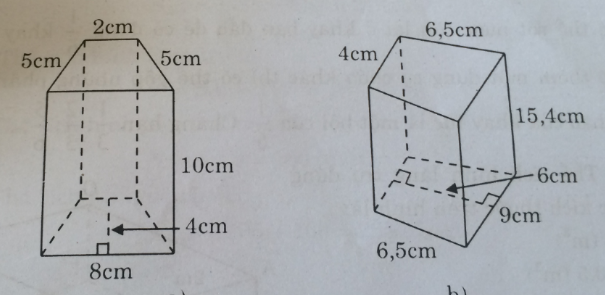
Tính thể tích và diện tích toàn phần của các hình lăng trụ đứng có các kích thước như trên hình 140.
Giải:
(hình 140 trang 147 sbt)
– Hình a:
Diện tích xung quanh bằng:
\({S_{xq}} = \left( {5 + 2 + 5 + 8} \right).10 = 200(c{m^2})\)
Diện tích đáy bằng:
Sđáy \( = {{\left( {2 + 8} \right)} \over 2}.4 = 20(c{m^2})\)
Diện tích toàn phần bằng:
STP = Sxq + 2.Sđáy \( = 200 + 2.20 = 240(c{m^2})\)
Thể tích lăng trụ đứng:
Advertisements (Quảng cáo)
\(V = S.h = 20.10 = 200(c{m^3})\)
– Hình b:
Diện tích xung quanh bằng:
\({S_{xq}} = \left( {4 + 6,5 + 9 + 6,5} \right).15,4 = 400,4(c{m^2})\)
Diện tích đáy bằng:
Sđáy \( = {{4 + 9} \over 2}.6 = 39(c{m^2})\)
Diện tích toàn phần bằng:
STP = Sxq + 2.Sđáy \( = 400,4 + 2.39 = 478,4(c{m^2})\)
Thể tích lăng trụ đứng:
\(V = S.h = 39.15,4 = 600,6(c{m^3})\)