Tính diện tích của hình được cho trong mỗi trường hợp sau đây:
a. Đa giác ABCDEF, biết AD = 4cm, BC = 1cm, FE = 2cm, FB = 3cm, FB vuông góc với AD như hình bs. 24
b. Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs. 25)
Biết AB = 13cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD

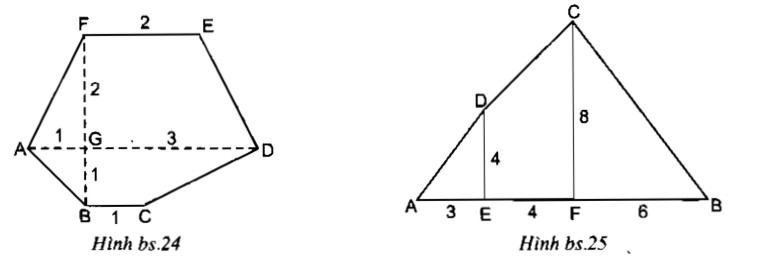
Ta chia đa giác ABCDEF thành hai hình thang ABCD và ADEF.
Hình thang ABCD có cạnh đáy BC = 1 (cm)
Advertisements (Quảng cáo)
Đáy AD = AG + GD = 1 + 3 = 4 (cm)
Đường cao BG = 1 (cm)
\({S_{ABCD}} = {{AD + BC} \over 2}.FG = {{4 + 1} \over 2} = {5 \over 2}\) (cm2)
Hình thang ADEF có đáy AD = 4 (cm)
Đáy EF = 2cm, đường cao FG = 2cm
\(\eqalign{ & {S_{ADEF}} = {{AD + EF} \over 2}.FG = {{4 + 2} \over 2}.2 = 6(c{m^2}) \cr & {S_{ABCDEF}} = {S_{ABCD}} + {S_{ADEF}} = {5 \over 2} + 6 = {{17} \over 2}(c{m^2}) \cr} \)
b. Chia đa giác ABCD thành tam giác vuông AED, hình thang vuông EDCF và tam giác vuông FCB.
\(\eqalign{ & {S_{AED}} = {1 \over 2}AE.DE = {1 \over 2}.3.4 = 6(c{m^2}) \cr & {S_{EDCF}} = {{ED + FC} \over 2}{\rm{.EF = }}{{4 + 8} \over 2}.4 = 24(c{m^2}) \cr & {S_{CFB}} = {1 \over 2}CF.FB = {1 \over 2}.8.6 = 24(c{m^2}) \cr & {S_{ABCD}} = {S_{AED}} + {S_{EDCF}} + {S_{CFB}} = 6 + 24 + 24 = 54(c{m^2}) \cr} \)
