Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs. 26.
Tính diện tích của đa giác đó, biết rằng : KH song song với BC (K thuộc EF); BC song song với GF; CF song song với BG; BG vuông góc với GF; CK song song với DE; CD song song với FE; KE = DE và KE vuông góc với DE; I là trung điểm của BH, AI = IH và AI vuông góc với IH; HK = 11cm, CF = 6cm. HK cắt CF tại J và JK = 3 (cm), JF = 2cm. BG cắt HK tại M và HM = 2cm.
Giải:
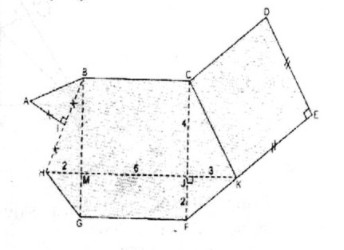
Chia đa giác đó thành hình vuông CDEK, hình thang KFGH, hình thang BCKH và tam giác vuông AIB
Ta có: MJ = KH – KJ – MH = 11 – 2 – 3 = 6(cm)
⇒ BC = GF = MJ = 6 (cm)
CJ = CF – FG = 6 – 2 = 4 (cm)
\(\eqalign{ & {S_{KFGH}} = {{HK + GF} \over 2}.FJ = {{11 + 6} \over 2}.2 = 17(c{m^2}) \cr & {S_{BCKH}} = {{BC + KH} \over 2}.CJ = {{11 + 6} \over 2}.4 = 34(c{m^2}) \cr} \)
Trong tam giác vuông CJK có \(\widehat J = 90^\circ \). Theo định lý Pi-ta-go ta có:
Advertisements (Quảng cáo)
\(C{K^2} = C{J^2} + J{K^2} = 16 + 9 = 25 \Rightarrow CK = 5\) (cm)
\({S_{CDEK}} = C{K^2} = {5^2} = 25\) (cm2 )
Trong tam giác vuông BMH có \(\widehat M = 90^\circ \).Theo định lý Pi-ta-go ta có:
\(B{H^2} = B{M^2} + H{M^2}\)
mà BM = CJ = 4(cm) (đường cao hình thang BCKH)
\(\eqalign{ & \Rightarrow B{H^2} = {4^2} + {2^2} = 20 \cr & IB = {{BH} \over 2} \Rightarrow I{B^2} = {{B{H^2}} \over 4} = {{20} \over 4} = 5 \cr & IB = \sqrt 5 (cm) \cr} \)
∆ AIB vuông cân tại I (vì AI = IH = IB)
\({S_{AIB}} = {1 \over 2}AI.IB = {1 \over 2}I{B^2} = {5 \over 2}\) ( cm2 )
\(S = {S_{CDEK}} + {S_{KFGH}} + {S_{BCKH}} + {S_{AIB}} = 25 + 17 + 34 + {5 \over 2} = {{157} \over 2}\) (cm2 )
