Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 8. Chứng minh rằng: \({S_{ABCD}} = {S_{AEFD}}.\). Bài 6. Diện tích đa giác
Cho hình thang ABCD \(\left( {AB//CD} \right)\). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng: \({S_{AOD}} = {S_{BOC}}.\)
b) Gọi M là trung điểm của BC. Từ M kẻ đường thẳng song song với AD cắt AB tại E và DC tại F.
Chứng minh rằng: \({S_{ABCD}} = {S_{AEFD}}.\)
a)
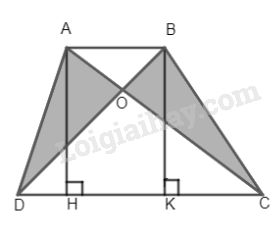
Ta có \({S_{ADC}} = {S_{DBC}}\) (chung đáy DC và đường cao AH = BK)
Advertisements (Quảng cáo)
\( \Rightarrow {S_{ADC}} - {S_{DOC}} = {S_{DBC}} - {S_{DOC}}\)
Hay \({S_{AOD}} = {S_{BOC}}.\)
b)
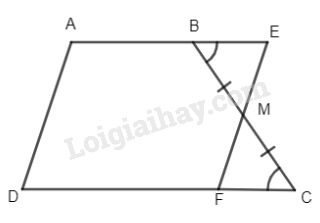
Ta có: \(\Delta BME = \Delta CMF(g.c.g)\)
\( \Rightarrow {S_{BME}} = {S_{CMF}}\)
\( \Rightarrow {S_{BME}} + {S_{ABMFD}} = {S_{CMF}} + {S_{ABMFD}}\)
Hay \({S_{AEFD}} = {S_{ABCD}}.\)