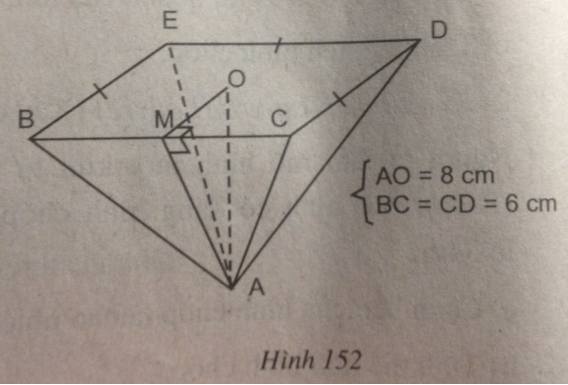
Tính diện tích toàn phần của hình chóp đều sau đây:
a. Hình cho theo các kích thước
trên hình 152.
b. Hình chóp tứ giác đều, cạnh đáy 6cm,
chiều cao hình chóp 5cm.
c. Hình chóp tứ giác đều, cạnh đáy 20cm,
chiều cao hình chóp 7cm.
d. Hình chóp tứ giác đều, cạnh đáy 1m,
chiều cao hình chóp 50cm.

a. Vì AO là đường cao hình chóp nên ∆ AOM vuông tại O.
Ta có: OM = \({1 \over 2}CD = 3(cm)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
\(\eqalign{ & A{M^2} = A{O^2} + O{M^2} \cr & = {8^2} + {3^2} = 73 \cr} \)
Suy ra: \(AM = \sqrt {73} (cm)\)
Ta có: \({S_{xq}} = Pd = 6.2.\sqrt {73} = 12\sqrt {73} (c{m^2})\)
Sđáy = 6.6 =36 (cm2)
Vậy STP = Sxq + Sđáy \( = 12\sqrt {73} + 36 \approx 138.5(c{m^2})\)
b. Hình chóp tứ giác đều, cạnh đáy bằng 6cm, chiều cao hình chóp bằng 5cm.
Tương tự hình vẽ câu a ta có MA ⊥ BC.
Vì AO là đường cao của hình chóp nên ∆ AOM vuông tại O.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
Advertisements (Quảng cáo)
\(\eqalign{ & A{M^2} = O{A^2} + O{M^2} \cr & = 25 + 9 = 34 \cr} \)
Suy ra:
Ta có: Sxq = \(6.2.\sqrt {34} = 12\sqrt {34} (c{m^2})\)
Sđáy = 6.6 = 36 (cm2)
Vậy STP = \(12\sqrt {34} + 36 \approx 106(c{m^2})\)
c. Hình chóp tứ giác đều, cạnh đáy bằng 20cm, chiều cao hình chóp bằng 7cm.
Tương tự hình vẽ câu a ta có: MA ⊥ BC
Vì AO là đường cao của hình chóp nên ∆ AOM vuông tại O.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
\(A{M^2} = A{O^2} + M{O^2} = {7^2} + {10^2} = 149\)
Suy ra: \(AM = \sqrt {149} (cm)\)
Ta có: \({S_{xq}} = 20.2.\sqrt {149} = 40\sqrt {149} (c{m^2})\)
Sđáy = \(20.20 = 400(c{m^2})\)
Vậy STP = Sxq + Sđáy = \(40\sqrt {149} + 400 \approx 888,3(c{m^2})\)
d. Hình chóp tứ giác đều, cạnh đáy bằng 1m, chiều cao hình chóp bằng 0,5m.
Tương tự hình vẽ câu a ta có: AM ⊥ BC.
Vì AO là đường cao của hình chóp nên ∆ AOM vuông tại O
Áp dụng định lí Pi-ta-go vào tam giác vuông AOM, ta có:
\(A{M^2} = A{O^2} + O{M^2} = {\left( {0,5} \right)^2} + {\left( {0,5} \right)^2} = 0,5\)
Suy ra: \(AM = \sqrt {0,5} (m)\)
Ta có: Sxq = \(1.2.\sqrt {0,5} = 2\sqrt {0,5} ({m^2})\)
Sđáy = 1.1 = 1 (m2)
Vậy \({S_{TP}} = 2\sqrt {0,5} + 1 \approx 2,4({m^2})\)
