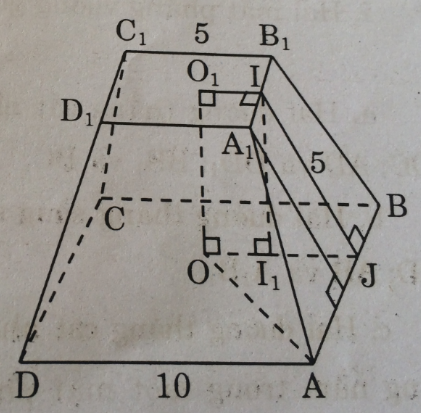
Cho hình chóp cụt tứ giác đều ABCD.A1B1C1D1 có các cạnh đáy 5cm và 10cm, đường cao của mặt bên bằng 5cm. Hãy tính:
a. Diện tích xung quanh của hình chóp cụt.
b. Tính cạnh bên và chiều cao của hình chóp cụt.
Giải:
(hình trang 163 sgbt)
a. Diện tích một mặt bên là hình thang bằng :
\(S = {1 \over 2}\left( {5 + 10} \right).5 = 37,5(c{m^2})\)
Diện tích xung quanh của hình chóp cụt đều là:
\({S_{xq}} = 4.37,5 = 150(c{m^2})\)
b. Kẻ A1H ⊥ AB, ta có:
A1I = 2,5cm; AJ = 5cm
Advertisements (Quảng cáo)
Suy ra: AH = 2,5cm
Áp dụng định lí Pi-ta-go vào tam giác vuông A1HA, ta có:
\({A_1}{A^2} = {A_1}{H^2} + A{H^2} = {5^2} + 2,{5^2} = 31,25\)
Suy ra: \({A_1}A = \sqrt {31,25} \approx 5,59(cm)\)
Ta có: \({O_1}I = 2,5cm;OJ = 5cm.\)
Kẻ II1 ⊥ OJ, suy ra I1J = 2,5cm
Áp dụng định lí Pi-ta-go vào tam giác vuông II1J, ta có:
\(I{J^2} = I{I_1}^2 + {{\rm I}_1}{J^2}\)
Suy ra: \(I{I_1}^2 = I{J^2} - {I_1}{J^2} = {5^2} - 2,{5^2} = 18,75\)
Suy ra: \(I{I_1} = \sqrt {18,75} \approx 4,33(cm)\)
Vậy O1O = II1 = 4,33 (cm)
