Tính diện tích toàn phần của hình chóp cụt đều cho theo các kích thước trên hình 154.

(hình 154 trang 153 sbt)
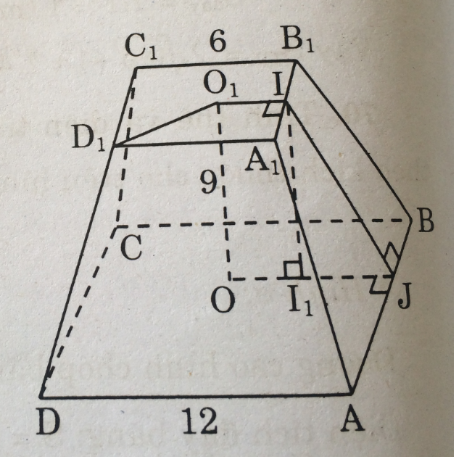
Ta có: A1D1 = 6 \( \Rightarrow {O_1}I = 3\)
\(AD = 12 \Rightarrow {\rm O}J = 6\)
Kẻ II1 ⊥ OJ, ta có: I1J = 3
Áp dụng định lí Pi-ta-go vào tam giác vuông II1J, ta có:
\(I{J^2} = I{I_1}^2 + {I_1}{J^2} = {9^2} + {3^2} = 90\)
Advertisements (Quảng cáo)
Suy ra:
Diện tích mặt một bên là một hình thang bằng:
\(S = {1 \over 2}\left( {6 + 12} \right).\sqrt {90} = 9\sqrt {90} \) (đvdt)
Diện tích xung quanh bằng : Sxq = \(4.9.\sqrt {90} = 36\sqrt {90} \) (đvdt)
Diện tích đáy trên bằng: S = 6.6 = 36 (đvdt)
Diện tích đáy dưới bằng: S = 12.12 = 144 (đvdt)
Diện tích toàn phần của hình chóp cụt là:
\({S_{TP}} = 36\sqrt {90} + 36 + 144 = \left( {36\sqrt {90} + 180} \right)\) (đvdt)
