Độ dài đường chéo AC1 (h.160) của một hình lập phương là \(\sqrt {12} \) .
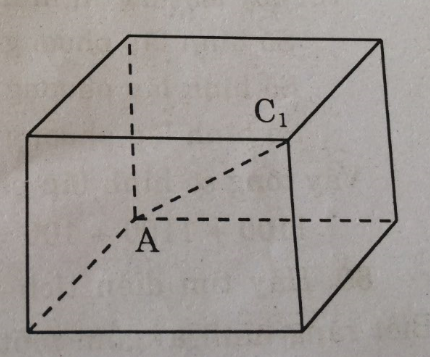
a. Độ dài mỗi cạnh là bao nhiêu ?
b. Tính diện tích toàn phần và thể tích
của hình lập phương.
Giải:
(hình 160 trang 155 sbt)
a. Gọi a là độ dài của hình lập phương. Vì là hình lập phương nên kích thước các cạnh bằng nhau.
Như vậy đường chéo đáy là đường chéo hình vuông cạnh a.
Advertisements (Quảng cáo)
Độ dài đường chéo đáy là \(a\sqrt 2 \)
Suy ra:
\(\eqalign{ & A{C_1}^2 = {\left( {a\sqrt 2 } \right)^2} + {a^2} \cr & = 2{a^2} + {a^2} = 3{a^2} \cr} \)
Mà \(A{C_1} = \sqrt {12} \) nên \(3{a^2} = 12 \Rightarrow {a^2} = 4 \Rightarrow a = 2\)
Vậy cạnh hình lập phương bằng 2 (đơn vị dài)
b. Diện tích toàn phần hình lập phương:
\({S_{TP}} = 6.\left( {2.2} \right) = 24\) (đơn vị diện tích)
Thể tích hình lập phương:
V = 2.2.2 = 8 (đơn vị thể tích)
