Câu 54 trang 97 SBT Toán 8 tập 2: ∆ AOB đồng dạng ∆ DOC...

Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, $\widehat {ABD} = \widehat {ACD}$.Gọi E là giao điểm của hai đường thẳng AD và BC (h.39)

Chứng minh rằng :

a. ∆ AOB đồng dạng ∆ DOC

b. ∆ AOD đồng dạng ∆ BOC

c. EA.ED = EB.EC

Giải:

(hình 39 trang 97 sbt)

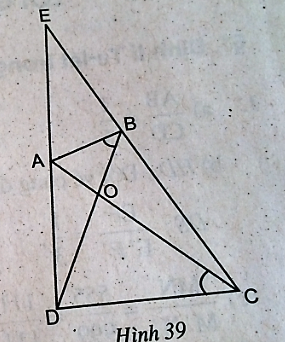
a. Xét ∆ AOB và ∆ DOC, ta có:

 $\widehat {ABD} = \widehat {ACD}$(gt)

Hay $\widehat {ABO} = \widehat {OCD}$

$\widehat {AOB} = \widehat {DOC}$  (đối đỉnh)

Vậy ∆ AOB đồng dạng ∆ DOC (g.g)

b. Vì ∆ AOB đồng dạng ∆ DOC nên:

${{AO} \over {DO}} = {{OB} \over {OC}} \Rightarrow {{AO} \over {OB}} = {{DO} \over {OC}}$

Xét ∆ AOD và ∆ BOC, ta có:

${{AO} \over {OB}} = {{DO} \over {OC}}$

$\widehat {AOD} = \widehat {BOC}$  (đối đỉnh)

Vậy ∆ AOD đồng dạng ∆ BOC (c.g.c)

c. Vì ∆ AOD đồng dạng ∆ BOC nên:

$\widehat {ADO} = \widehat {BCO}$

hay $\widehat {EDB} = \widehat {ECA}$

Xét ∆ EDB và ∆ ECA, ta có:

$\widehat E$ chung

$\widehat {EDB} = \widehat {ECA}$  (chứng minh trên )

Vậy ∆ EDB đồng dạng ∆ ECA (g.g)

Suy ra: ${{ED} \over {EC}} = {{EB} \over {EA}} \Rightarrow ED.EA = EC.EB$