Cho tam giác ABC vuông tại A, điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, gọi F là điểm đối xứng với D qua AC. Chứng minh rằng các điểm E và F đối xứng nhau qua điểm A.
Giải:
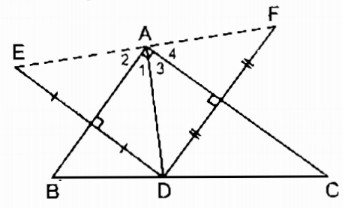
Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
nên ∆ ADE cân tại A
Suy ra: AB là đường phân giác của \(\widehat {DAE} \Rightarrow {\widehat A_1} = \widehat {{A_2}}\)
Vì F đối xứng với D qua AC
Advertisements (Quảng cáo)
⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF ( tính chất đường trung trực)
nên ∆ ADF cân tại A
Suy ra: AC là đường phân giác của \(\widehat {DAF}\)
\( \Rightarrow {\widehat A_3} = {\widehat A_4}\)
\(\widehat {EAF} = \widehat {EAD} + \widehat {{\rm{DAF}}} = {\widehat A_2} + {\widehat A_1} + {\widehat A_3} + {\widehat A_4}\)
\(= 2\left( {{{\widehat A}_1} + {{\widehat A}_3}} \right) = {2.90^0} = {180^0}\)
⇒ E, A, F thẳng hàng có AE = AF = AD
nên A là trung điểm của EF hay điểm E đối xứng với F qua điểm A.
