Chứng minh rằng các điểm E và F đối xứng nhau qua điểm O.. Câu 96 trang 92 Sách bài tập (SBT) Toán 8 tập 1 - Bài 8. Đối xứng tâm
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt hai cạnh đối AD, BC ở E, F. Chứng minh rằng các điểm E và F đối xứng nhau qua điểm O.

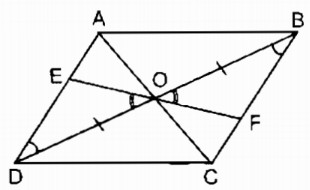
Xét ∆ OED và ∆ OFB:
\(\widehat {EOD} = \widehat {FOB}\) (đối đỉnh)
Advertisements (Quảng cáo)
OD = OB (tính chất hình bình hành)
\(\widehat {ODE} = \widehat {OBF}\) (so le trong)
Do đó: ∆ OED = ∆ OFB (g.c.g)
⇒ OE = OF
nên O là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm O.
