Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC.
a. Chứng minh rằng ADEF là hình thoi
b. Tam giác ABC có thêm điều kiện gì thì ADEF là hình vuông ?
Giải:
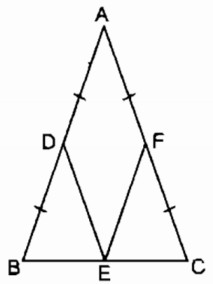
a. Ta có: E là trung điểm của BC (gt)
D là trung điểm của AB (gt)
nên ED là đường trung bình của ∆ ABC
DE = AF = \({1 \over 2}\)AC (1)
F là trung điểm của AC (gt)
Advertisements (Quảng cáo)
nên EF là đường trung bình ∆ ABC ⇒ EF = AD = \({1 \over 2}\)AB (2)
AB = AC (gt)
Từ (1), (2) và (gt) suy ra: AD = DE = EF = AF
Vậy tứ giác ADEF là hình thoi.
b. Hình thoi ADEF là hình vuông ⇒ \(\widehat A = {90^0}\)
⇒ ∆ ABC vuông cân tại A
Ngược lại nếu ∆ ABC vuông cân tại A
⇒ Tứ giác ADEF là hình thoi có \(\widehat A = {90^0}\)
⇒ Hình thoi ADEF là hình vuông
Vậy hình thoi ADEF là hình vuông thì ∆ ABC vuông cân tại A.
