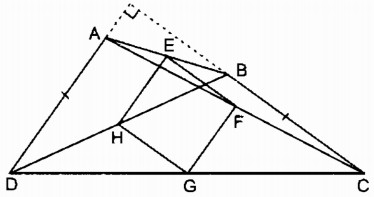
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, DC, DB. Tìm điều kiện của tứ giác ABCD để EFGH là. Câu 160 trang 100 Sách bài tập (SBT) Toán 8 tập 1 - Bài tập ôn chương I - Tứ giác
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, DC, DB. Tìm điều kiện của tứ giác ABCD để EFGH là:
a. Hình chữ nhật
b. Hình thoi
c. Hình vuông

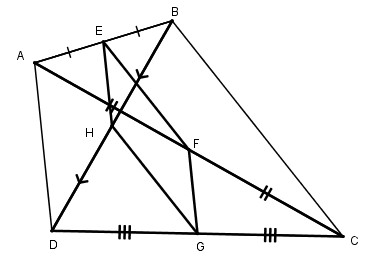
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF // BC, EF = \({1 \over 2}\) BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Advertisements (Quảng cáo)
Nên HG // BC, HG = \({1 \over 2}\) BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
a) EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AD ⊥ BC
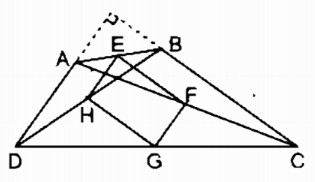
b) EFGH là hình thoi ⇔ EH = EF ⇔ AD = BC
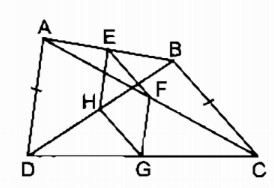
c) EFGH là hình thoi ⇔ AD ⊥ BC và AD = BC