Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC.
a. Chứng minh rằng D đối xứng với E qua A
b. Tam giác DHE là tam giác gì ? Vì sao ?
c. Tứ giác BDEC là hình gì ? Vì sao ?
d. Chứng minh rằng BC = BD + CE.
Giải:
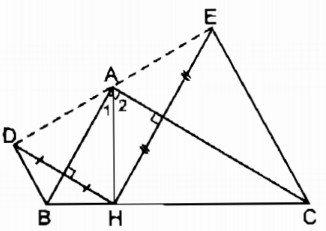
a. Điểm D đối xứng điểm H qua trục AB
⇒ AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực) ⇒ ∆ ADH cân tại A
Advertisements (Quảng cáo)
Suy ra: AB là tia phân giác của \(\widehat {DAH} \Rightarrow \widehat {DAB} = {\widehat A_1}\)
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A
Suy ra: AC là đường phân giác của \(\widehat {HAE} \Rightarrow {\widehat A_2} = \widehat {EAC}\)
\(\widehat {DAE} = \widehat {DAH} + \widehat {HAE} = 2\left( {{{\widehat A}_1} + {{\widehat A}_2}} \right) = {2.90^0} = {180^0}\)
D, A, E thẳng hàng
AD = AE (vì cùng bằng AH)
nên điểm A là trung điểm của đoạn DE
Vậy điểm D đối xứng với điểm E qua điểm A.
