
Cho tam giác ABC cân tại A có hai đường phân giác BE và CK. Chứng minh tứ giác BKEC là hình thang cân.

Chứng minh BKEC là hình thang có \(\widehat {ABC} = \widehat {ACB}\)

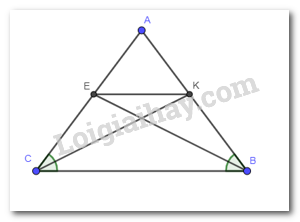
Do BE là phân giác của \(\widehat {ABC}\)nên \[\widehat {{B_1}} = \widehat {{B_2}} = \frac{{\widehat {ABC}}}{2}\]
CK là phân giác của \(\widehat {ACB}\) nên \(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat {ACB}}}{2}\)
Advertisements (Quảng cáo)
Mà: \(\widehat {ABC} = \widehat {ACB} = \frac{{{{180}^0} - \widehat A}}{2}(1)\)(do \(\Delta ABC\)cân tại A)
\( \Rightarrow \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)
Xét \(\Delta AEB\)và \(\Delta AKC\)có: \(\widehat A\)chung, \(\widehat {{B_1}} = \widehat {{C_1}}\)
AB = AC \( \Rightarrow \Delta AEB = \Delta AKC(g.c.g)\)
\( \Rightarrow AE = AK \Rightarrow \Delta AEK\)cân tại A.. \(\widehat {AEK} = \widehat {AKE} = \frac{{{{180}^0} - \widehat A}}{2}(2)\)
Từ (1), (2) suy ra: \(\widehat {ABC} = \widehat {AKE} \Rightarrow KE//BC\)(2 góc đơn vị)
Suy ra BKEC là hình thang (3)
Từ (1), (3) suy ra BKEC là hình thang cân.
