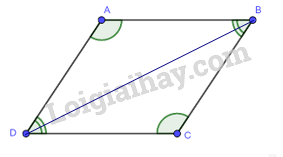
Cho tứ giác ABCD có \(\widehat {DAB} = \widehat {BC{\rm{D}}};\widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\). Chứng minh ABCD là hình bình hành.
Chứng minh tứ giác ABCD có các cặp cạnh đối bằng nhau
Xét \(\Delta ABD\)có: \(\widehat {BAD} + \widehat {ABD} + \widehat {BDA} = {180^0}\)
Xét \(\Delta BCD\)có: \(\widehat {BCD} + \widehat {BDC} + \widehat {DBC} = {180^0}\)
\(\begin{array}{l} \Rightarrow \widehat {BAD} + \widehat {ABD} + \widehat {BDA} = \widehat {BCD} + \widehat {BDC} + \widehat {DBC}\\ \Rightarrow \widehat {DAB} = \widehat {DBC}(do\,\widehat {BAD} = \widehat {BCD};\widehat {ABD} = \widehat {BDC})\end{array}\)
Xét \(\Delta ABD\) và \(\Delta CDB\) có:
\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABD} = \widehat {CDB}\\BDchung\\\widehat {DBA} = \widehat {DBC}\end{array} \right\} \Rightarrow \Delta ABD = \Delta CDB(g.c.g)\\ \Rightarrow AB = DC\\AD = CB\end{array}\)
Suy ra tứ giác ABCD là hình bình hành vì có cặp cạnh đối bằng nhau