Hoạt động3
Cho hình thang cân ABCD có AB // CD , AB < CD, E là giao điểm của AD và BC (Hình 25)
a) So sánh các cặp góc: \(\widehat {E{\rm{D}}C}\) và \(\widehat {EC{\rm{D}}}\); \(\widehat {E{\rm{A}}B}\) và \(\widehat {EBA}\).
b) So sánh các cặp đoạn thẳng: EA và EB, ED và EC. Từ đó, hãy so sánh AD và BC.
c) Hai tam giác ADC và BCD có bằng nhau hay không? Từ đó, hãy so sánh AC và BD
Quan sát hình 25.
a, Do ABCD là hình thang cân nên.
\(\widehat {ADC} = \widehat {BCD}\)hay \(\widehat {EDC} = \widehat {ECD}\)
Do ABCD là hình thang cân nên
\(\widehat {BAD} = \widehat {ABC}\left( 1 \right)\)
Mà:
\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = {180^0}\\\widehat {ABC} + \widehat {EBA} = {180^0}\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = \widehat {ABC} + \widehat {EBC}\\ \Rightarrow \widehat {EAB} = \widehat {EBA}\end{array}\)(do(1))
b, Do \(\widehat {EAB} = \widehat {EBA}\) suy ra \(\Delta EAB\)cân tại E nên EA = EB
Do \(\widehat {EDC} = \widehat {ECD}\) suy ra \(\Delta ECD\)cân tại E nên ED = EC
Mà: ED = EC
Suy ra EA + AD = EB + BC
Suy ra AD = BC (do EA = EB)
c, Xét \(\Delta ADC\) và \(\Delta BCD\) có:
AD = BC
\(\widehat {ADC} = \widehat {BCD}\)
DC chung
Suy ra: \(\Delta ADC = \Delta BCD(c.g.c) \Rightarrow AC = BD\)
Luyện tập1
Cho hình thang cân, ABCD có AB //CD. Chứng minh \(\widehat {A{\rm{DB}}} = \widehat {BCA}\)
Chứng minh \(\Delta ADB = \Delta BCA(c.g.c)\)
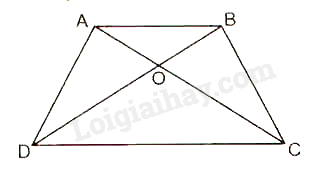
Do tứ giác ABCD là hình thang cân nên
AD = BC.
AC = BD.
Xét \(\Delta ADB\) và \(\Delta BCA\) có:
AB chung, AD = BC, AC = BD
\(\Rightarrow \Delta ADB=\Delta BCA\) (c.c.c)