Hoạt động4
Quan sát hình thang ABCD (AB //CD, AB < CD) có hai đường chéo AC và BD bằng nhau kẻ BE song song với AC (E thuộc đường thẳng CD) như hình 27
a) Hai tam giác ABC và ECB có bằng nhau hay không?
b) So sánh các cặp góc: \(\widehat {BE{\rm{D}}}\) và \(\widehat {B{\rm{D}}E};\widehat {AC{\rm{D}}}\) và \(\widehat {BE{\rm{D}}}\)
c) Hai tam giác ACD và BDC có bằng nhau không? Từ đó, hãy so sánh \(\widehat {A{\rm{D}}C}\) và \(\widehat {BC{\rm{D}}}\).
d) ABCD có phải là hình thang cân hay không?

a, chứng minh \(\Delta ABC = \Delta ECB(g.c.g)\)
b, \(\widehat {BED} = \widehat {BAC} = \widehat {BDE}\)

Do ABCD là hình thang nên AB//CD.
Kẻ BE//AC, \(E \in CD\) nên CE//AB.
\( \Rightarrow \widehat {BCE} = \widehat {ABC}\); \(\widehat {CBE} = \widehat {ACB}\) (hai góc so le trong).
a, Xét \(\Delta ABC\)và \(\Delta ECB\) có:
\(\widehat {BCE} = \widehat {ABC}\)
BC chung
\(\widehat {CBE} = \widehat {ACB}\) (do BC//AC )
\( \Rightarrow \Delta ABC = \Delta ECB\)(g.c.g)
b, BE = AC = BD
\( \Rightarrow \Delta BDE\)cân tại B
\( \Rightarrow \widehat {BDE} = \widehat {BED}\)
Do \(\Delta ABC = \Delta ECB\)
\( \Rightarrow \widehat {BEC} = \widehat {BAC}\) (2 góc tương ứng) hay \(\widehat {BED} = \widehat {BAC}(1)\)
Mà: \(\widehat {BAC} = \widehat {ACD}\) (do AB//CD) (2)
Từ (1), (2) suy ra: \(\widehat {BED} = \widehat {ACD}\)
c, Theo câu b:
\(\begin{array}{l}\widehat {BED} = \widehat {BDE}\\\widehat {ACD} = \widehat {BED}\end{array}\) suy ra: \(\widehat {ACD} = \widehat {BDE}\) hay \(\widehat {ACD} = \widehat {BDC}\)
Advertisements (Quảng cáo)
Xét \(\Delta ACD\)và \(\Delta BDC\)có:
CD chung
\(\widehat {ACD} = \widehat {BDC}\)
AC = BD (gt)
\( \Rightarrow \Delta ACD = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {ADC} = \widehat {BCD}\) (2 góc tương ứng)
d, Hình thang ABCD (AB//CD) có \(\widehat {ADC} = \widehat {BCD}\)nên hình thang ABCD là hình thang cân.
Luyện tập2
Một ô cửa sổ có dạng hình chữ nhật với chiều dài là 120 m và chiều rộng là 80 cm. Người ta mở rộng ô cửa sổ đó bằng cách tăng độ dài cạnh dưới về hai bên, mỗi bên 20 cm (mô tả ở Hình 29). Sau khi mở rộng thì ô của sổ đó có dạng hình gì? Tính diện tích của ô của sổ đó sau khi mở rộng.

Quan sát hình 29 sau khi mở rộng thì ô cửa đó có dạng hình thang cân.

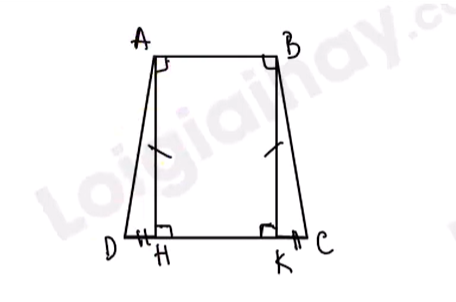
Xét \(\Delta AHD\) và \( \Delta BKC\) có:
\(\widehat {AHD} =\widehat{BKC} = 90^0\)
AH = BK
HD = KC
\( \Rightarrow \Delta AHD = \Delta BKC (c.g.c) \Rightarrow \widehat{ADH} = \widehat{BCK}\)
Do AB // KH hay AB // CD suy ra ABCD là hình thang.
Mà \(\widehat{ADH} = \widehat{BCK}\) (cmt)
Suy ra ABCD là hình thang cân.
Ta có: AB = HK = 80 (cm)
DC = DH + HK + KC = 20 + 80 + 20 = 120 (cm).
Chiều cao của hình thang ABCD là 120 cm (= BK).
=> Diện tích của ô cửa sổ sau khi mở rộng là:
\( S = \frac{1}{2}(AB + CD).BK = \frac{1}{2}(80 + 120).120 = 12000(cm^2)\)
