Hướng dẫn trả lời bài 2 trang 71 SGK Toán 8 – Chân trời sáng tạo Bài 3. Hình thang - Hình thang cân. Cho tứ giác \(ABCD\) có \(AB = AD\), \(BD\) là tia phân giác của góc \(B\).
Cho tứ giác \(ABCD\) có \(AB = AD\), \(BD\) là tia phân giác của góc \(B\). Chứng minh rằng \(ABCD\) là hình thang.
Chứng minh \(AD\) // \(BC\)
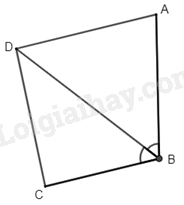
Xét \(\Delta ABD\) ta có: \(AD = AB\) (gt)
\( \Rightarrow \Delta ADB\) cân tại \(A\)
\( \Rightarrow \widehat {ADB} = \widehat {ABD}\)
Mà \(\widehat {ABD} = \widehat {CBD}\) (do \(BD\) là phân giác của góc \(B\))
\( \Rightarrow \widehat {ADB} = \widehat {CBD}\)
Mà hai góc ở vị trí so le trong
\( \Rightarrow AD\;{\rm{//}}\;BC\)
Suy ra \(ABCD\) là hình thang