a) Chứng minh \(NM\) // \(BC\) rồi chỉ ra \(BNMC\) là hình thangb) Chứng minh \(\Delta BNM\) cân tại \(N\) Giải và trình bày phương pháp giải bài 3 trang 71 SGK Toán 8 – Chân trời sáng tạo Bài 3. Hình thang - Hình thang cân. Cho tam giác nhọn...
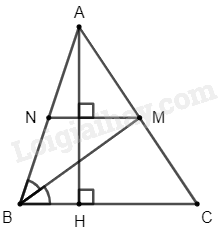
Cho tam giác nhọn \(ABC\) có \(AH\) là đường cao. Tia phân giác của góc \(B\) cắt \(AC\) tại \(M\). Từ \(M\) kẻ đường thẳng vuông góc với \(AH\) và cắt \(AB\) tại \(N\). Chứng minh rằng:
a) Tứ giác \(BCMN\) là hình thang
b) \(BN = MN\)
a) Chứng minh \(NM\) // \(BC\) rồi chỉ ra \(BNMC\) là hình thang
b) Chứng minh \(\Delta BNM\) cân tại \(N\)
a) Ta có:
Advertisements (Quảng cáo)
\(NM \bot AH\) (gt)
\(BC \bot AH\) (gt)
Suy ra \(NM\) // \(BC\)
Suy ra \(BNMC\) là hình thang
b) Vì \(NM\) // \(BC\) (cmt)
Suy ra \(\widehat {{\rm{NMB}}} = \widehat {{\rm{MBC}}}\) (so le trong)
Mà \(\widehat {{\rm{MBN}}} = \widehat {{\rm{MBC}}}\) (do \(MB\) là phân giác)
Suy ra \(\widehat {{\rm{MBN}}} = \widehat {{\rm{NMB}}}\)
Suy ra \(\Delta MNB\) cân tại \(N\)
Suy ra \(BN = NM\)