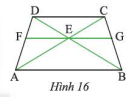
Cho hình thang cân \(ABCD\) có \(AB\) // \(CD\). Qua gia điểm \(E\) của \(AC\) và \(BD\), ta vẽ đường thẳng song song với \(AB\) và cắt \(AD\), \(BC\) lần lượt tại \(F\) và \(G\) (Hình 16). Chứng minh rằng \(EG\) là tia phân giác của góc \(CEB\).
Chứng minh \(\widehat {{\rm{CEG}}} = \widehat {{\rm{BEG}}}\)
Vì \(EG\) // \(AB\) (gt)
suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{CAB}}}\) (đồng vị) và \(\widehat {{\rm{GEB}}} = \widehat {{\rm{EBA}}}\) (1)
Xét \(\Delta CAB\) và \(\Delta DBA\) ta có:
\(AC = BD\) (tính chất hình thang cân)
\(BC = AD\) (tính chất hình thang cân)
\(AB\) chung
Suy ra \(\Delta CAB = \Delta DBA\) (c-c-c)
Suy ra \(\widehat {{\rm{CAB}}} = \widehat {{\rm{EAB}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{GEB}}}\)
Suy ra \(EG\) là phân giác của \(\widehat {{\rm{CEB}}}\)