Lời giải bài tập, câu hỏi bài 7 trang 51 SGK Toán 8 tập 2– Chân trời sáng tạo Bài 1. Định lí Thalès trong tam giác. Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\).

Cho hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Chứng minh rằng \(OA.OD = OB.OC\)

Sử dụng hệ quả của định lí Thales.
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Advertisements (Quảng cáo)

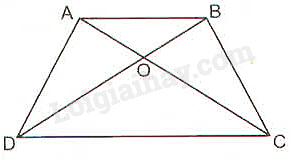
Xét tam giác \(OCD\) có \(AB//CD\) (giả thiết) và \(AB\) cắt \(OC;OD\) lần lượt tại \(A;B\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{AB}}{{CD}} \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} \Rightarrow OA.OD = OB.OC\) (điều phải chứng minh).
