Lời giải bài tập, câu hỏi bài 7 trang 71 SGK Toán 8 tập 2– Chân trời sáng tạo Bài 2. Các trường hợp đồng dạng của hai tam giác. Trong Hình 19, cho biết \(MN//BC, MB//AC\) Chứng minh rằng \(\Delta BNM\backsim\Delta ABC\) Tính \(\widehat C\) :
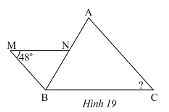
Trong Hình 19, cho biết \(MN//BC,MB//AC\)
a) Chứng minh rằng \(\Delta BNM\backsim\Delta ABC\)
b) Tính \(\widehat C\)
- Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau.
- Hai tam giác đồng dạng thì các góc tương ứng bằng nhau.
Advertisements (Quảng cáo)
a) Vì \(MN//BC\) nên \(\widehat {MNB} = \widehat {CBA}\) (hai góc so le trong)
Vì \(MB//AC\) nên \(\widehat {MBN} = \widehat {CAB}\) (hai góc so le trong)
Xét tam giác \(BNM\) tam giác \(ABC\) ta có:
\(\widehat {MNB} = \widehat {CBA}\) (chứng minh trên)
\(\widehat {MBN} = \widehat {CAB}\) (chứng minh trên)
Do đó, \(\Delta BNM\backsim\Delta ABC\) (g.g)
b) Vì \(\Delta BNM\backsim\Delta ABC\) nên \(\widehat M = \widehat C = 48^\circ \) (hai góc tương ứng).