Hoạt động1
a) Cho đoạn thẳng \(AB\) và điểm \(O\). Kẻ các tia \(OA,OB\). Trên tia \(OA,OB\) lần lượt lấy các điểm \(A’,B’\) sao cho \(OA’ = 3OA,OB’ = 3OB\) (ình 1a).
i) \(A’B’\) có song song với \(AB\) không.
ii) Tính tỉ số \(\frac{{A’B’}}{{AB}}\).
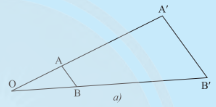
b) Cho tam giác \(ABC\) và điểm \(O\). Kẻ các tia \(OA,OB,OC\). Trên tia \(OA,OB,OC\) lần lượt lấy các điểm \(A’,B’,C’\) sao cho \(OA’ = 3OA,OB’ = 3OB,OC’ = 3OC\) (Hình 1b).
i) Tính và so sánh các tỉ số \(\frac{{A’B’}}{{AB}},\frac{{A’C’}}{{AC}},\frac{{B’C’}}{{BC}}\).
ii) Chứng minh tam giác \(A’B’C’\) đồng dạng với tam giác \(ABC\).
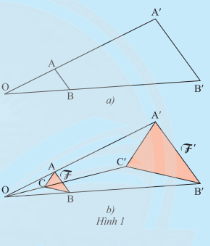

- Sử dụng định lí Thales đảo;
- Sử dụng hệ quả của định lí Thales;
- Sử dụng trường hợp đồng dạng thứ nhất của tam giác (c.c.c)

a)
i) Vì \(OA’ = 3OA \Rightarrow \frac{{OA}}{{OA’}} = \frac{1}{3}\);\(OB’ = 3OB \Rightarrow \frac{{OB}}{{OB’}} = \frac{1}{3}\).
Xét tam giác \(OA’B’\) có:
\(\frac{{OA}}{{OA’}} = \frac{{OB}}{{OB’}} = \frac{1}{3}\)
Do đó, \(A’B’//AB\) (định lí Thales đảo)
ii) Vì \(A’B’//AB \Rightarrow \frac{{OA}}{{OA’}} = \frac{{OB}}{{OB’}} = \frac{{AB}}{{A’B’}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A’B’}}{{AB}} = \frac{3}{1} = 3\).
b)
i)
- Vì \(OA’ = 3OA \Rightarrow \frac{{OA}}{{OA’}} = \frac{1}{3}\);\(OB’ = 3OB \Rightarrow \frac{{OB}}{{OB’}} = \frac{1}{3}\).
Xét tam giác \(OA’B’\) có:
\(\frac{{OA}}{{OA’}} = \frac{{OB}}{{OB’}} = \frac{1}{3}\)
Do đó, \(A’B’//AB\) (định lí Thales đảo)
Vì \(A’B’//AB \Rightarrow \frac{{OA}}{{OA’}} = \frac{{OB}}{{OB’}} = \frac{{AB}}{{A’B’}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A’B’}}{{AB}} = \frac{3}{1} = 3\).
- Vì \(OA’ = 3OA \Rightarrow \frac{{OA}}{{OA’}} = \frac{1}{3}\);\(OC’ = 3OC \Rightarrow \frac{{OC}}{{OC’}} = \frac{1}{3}\).
Xét tam giác \(OA’C’\) có:
\(\frac{{OA}}{{OA’}} = \frac{{OC}}{{OC’}} = \frac{1}{3}\)
Do đó, \(A’C’//AC\) (định lí Thales đảo)
Vì \(A’C’//AC \Rightarrow \frac{{OA}}{{OA’}} = \frac{{OC}}{{OC’}} = \frac{{AC}}{{A’C’}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A’C’}}{{AC}} = \frac{3}{1} = 3\).
- Vì \(OB’ = 3OB \Rightarrow \frac{{OB}}{{OB’}} = \frac{1}{3}\);\(OC’ = 3OC \Rightarrow \frac{{OC}}{{OC’}} = \frac{1}{3}\).
Xét tam giác \(OB’C’\) có:
\(\frac{{OB}}{{OB’}} = \frac{{OC}}{{OC’}} = \frac{1}{3}\)
Do đó, \(B’C’//BC\) (định lí Thales đảo)
Vì \(B’C’//BC \Rightarrow \frac{{OB}}{{OB’}} = \frac{{OC}}{{OC’}} = \frac{{BC}}{{B’C’}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{B’C’}}{{BC}} = \frac{3}{1} = 3\).
Do đó, \(\frac{{B’C’}}{{BC}} = \frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}}\)
ii) Xét tam giác \(A’B’C’\) và tam giác \(ABC\) ta có:
Advertisements (Quảng cáo)
\(\frac{{B’C’}}{{BC}} = \frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}}\) (chứng minh trên)
Do đó, tam giác \(A’B’C’\) đồng dạng với tam giác \(ABC\).
Hoạt động2
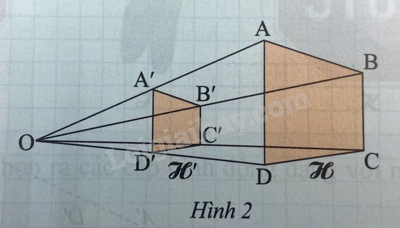
Cho tứ giác ABCD và điểm O(O không thuộc các đường thẳng AB, BC, CD, DA). Trên các tia \(OA,OB,OC,OD\) lần lượt lấy các điểm \(A’,B’,C’,D’\) sao cho \(OA’ = \frac {1}{2} OA,OB’ = \frac {1}{2} OB,OC’ = \frac {1}{2} OC,OD’ = \frac {1}{2} OD\) (Hình 2).
Tính và so sánh các tỉ số \(\frac{{A’B’}}{{AB}};\frac{{A’D’}}{{AD}};\frac{{B’C’}}{{BC}};\frac{{C’D’}}{{CD}}\).

- Ta thực hiện các phép tính tỉ số.
- Sử dụng định lí Thales đảo;
- Sử dụng hệ quả của định lí Thales;

- Vì \(OA’ = \frac {1}{2} OA \Rightarrow \frac{{OA’}}{{OA}} = \frac{1}{2}\);\(OB’ = \frac {1}{2} OB \Rightarrow \frac{{OB’}}{{OB}} = \frac{1}{2}\).
Xét tam giác \(OAB\) có:
\(\frac{{OA’}}{{OA}} = \frac{{OB’}}{{OB}} = \frac{1}{2}\)
Do đó, \(A’B’//AB\) (định lí Thales đảo)
Vì \(A’B’//AB \Rightarrow \frac{{OA’}}{{OA}} = \frac{{OB’}}{{OB}} = \frac{{A’B’}}{{AB}} = \frac{1}{2}\) (hệ quả của định lí Thales)
- Vì \(OA’ = \frac {1}{2} OA \Rightarrow \frac{{OA’}}{{OA}} = \frac{1}{2}\);\(OD’ = \frac {1}{2}OD \Rightarrow \frac{{OD’}}{{OD}} = \frac{1}{2}\).
Xét tam giác \(OAD\) có:
\(\frac{{OA’}}{{OA}} = \frac{{OD’}}{{OD}} = \frac{1}{2}\)
Do đó, \(A’D’//AD\) (định lí Thales đảo)
Vì \(A’D’//AD \Rightarrow \frac{{OA’}}{{OA}} = \frac{{OD’}}{{OD}} = \frac{{A’D’}}{{AD}} = \frac{1}{2}\) (hệ quả của định lí Thales)
- Vì \(OB’ = \frac {1}{2} OB \Rightarrow \frac{{OB’}}{{OB}} = \frac{1}{2}\);\(OC’ = \frac {1}{2} OC \Rightarrow \frac{{OC’}}{{OC}} = \frac{1}{2}\).
Xét tam giác \(OBC\) có:
\(\frac{{OB’}}{{OB}} = \frac{{OC’}}{{OC}} = \frac{1}{2}\)
Do đó, \(B’C’//BC\) (định lí Thales đảo)
Vì \(B’C’//BC \Rightarrow \frac{{OB’}}{{OB}} = \frac{{OC’}}{{OC}} = \frac{{B’C’}}{{BC}} = \frac{1}{2}\) (hệ quả của định lí Thales)
- Vì \(OD’ = \frac {1}{2} OD \Rightarrow \frac{{OD’}}{{OD}} = \frac{1}{2}\);\(OC’ = \frac {1}{2}OC \Rightarrow \frac{{OC’}}{{OC}} = \frac{1}{2}\).
Xét tam giác \(ODC\) có:
\(\frac{{OD’}}{{OD}} = \frac{{OC’}}{{OC}} = \frac{1}{2}\)
Do đó, \(D’C’//DC\) (định lí Thales đảo)
Vì \(D’C’//DC \Rightarrow \frac{{OD’}}{{OD}} = \frac{{OC’}}{{OC}} = \frac{{D’C’}}{{DC}} = \frac{1}{2}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{B’C’}}{{BC}} = \frac{{A’B’}}{{AB}} = \frac{{C’D’}}{{CD}} = \frac{{A’D’}}{{AD}}\).
Thực hành1
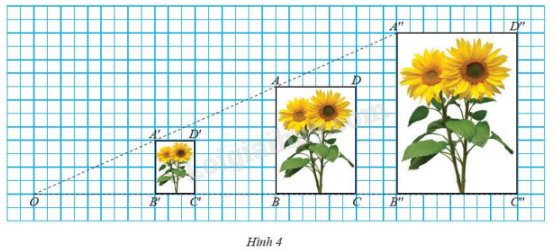
Cho ba tấm ảnh được đặt trên lưới ô vuông như Hình 4. Hãy chỉ ra ba cặp hình, trong mỗi cặp hình này đồng dạng phối cảnh với hình kia và chỉ ra tỉ số đồng dạng tương ứng.

Học sinh quan sát và tiến hành đo độ dài các cạnh của hình.
Nếu các cặp tỉ số của các cạnh tương ứng bằng nhu thì các cặp hình này đồng dạng.

Ta tiến hành đo và nhận thấy hình \(ABCD\) là hình đồng dạng phối cảnh với hình \(A’B’C’D’\) theo tỉ số \(k = \frac {AB}{A’B’} = \frac {BC}{B’C’} = \frac {8}{4} = \frac {6}{3} = 2\).
Ta tiến hành đo và nhận thấy hình \(A’B’C’D’\) là hình đồng dạng phối cảnh với hình \(A”B”C”D”\) theo tỉ số \(k = \frac {A’B’}{A”B”} = \frac {B’C’}{B”C”} = \frac {4}{12} = \frac {3}{9} = \frac {1}{3}\).
=> Hình \(ABCD\) đồng dạng phối cảnh với hình \(A”B”C”D”\) theo tỉ số \( k = 2.\frac {1}{3} = \frac {2}{3} \)
