Hoạt động 4
Hình 11a là hình chụp tấm lưới thép được đan thành nhiều mắt. Hình 11b là hình vẽ phóng to của một mắt lưới. Đo độ dài các cạnh của tứ giác \(ABCD\) và rút ra nhận xét.


Sử dụng thước đo độ dài các cạnh của tứ giác

Các cạnh của tứ giác \(ABCD\) có độ dài bằng nhau
Hoạt động 5
a) Hình thoi có là hình bình hành không?
b) Cho hình thoi \(ABCD\) có \(O\) là giao điểm của hai đường chéo (Hình 13b). Các tam giác \(OAB\), \(OCB\), \(OCD\), \(OAD\) có bằng nhau không?
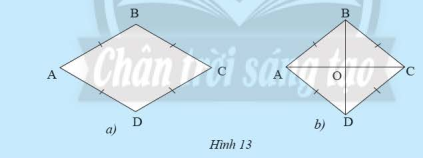

a) Áp dụng dấu hiệu nhận biết của hình bình hành
b) Áp dụng trường hợp bằng nhau thứ nhất của tam giác

a) Hình thoi cũng là hình bình hànhs
b) Vì \(ABCD\) là hình thoi (gt)
Suy ra \(ABCD\) cũng là hình bình hành
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Suy ra \(OA = OC\); \(OB = OD\)
Các tam giác \(OAB\); \(OCB\); \(OCD\); \(OAD\) bằng nhau theo trường hợp c-c-c
Thực hành 3
Cho hình thoi \(MNPQ\) có \(I\) là giao điểm của hai đường chéo.
a) Tính \(MP\) khi biết \(MN = 10\)dm, \(IN = 6\)dm
b) Tính \(\widehat {{\rm{IMN}}}\) khi \(\widehat {{\rm{MNP}}} = 128^\circ \)

Sử dụng tính chất của hình thoi

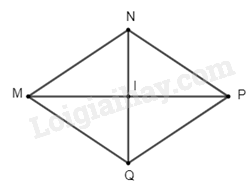
a) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(IM = IP\) và \(NQ \bot MP\)
Suy ra \(\widehat {{\rm{MIN}}} = 90\)
Xét tam giác vuông \(MPI\) (vuông tại \(I\)) ta có:
\(M{I^2} = M{N^2} - N{I^2} = {10^2} - {6^2} = 100 - 36 = 64\) (định lý Pythagore)
Suy ra \(MI = 8\) (dm)
b) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(NI\) là phân giác của \(\widehat {MNP}\)
Suy ra \(\widehat {MNI} = \widehat {PNI} = \frac{{128^\circ }}{2} = 64^\circ \)
Xét \(\Delta MNI\) vuông tại \(I\) ta có:
\(\widehat {{\rm{MNI}}} + \widehat {{\rm{NMI}}} = 90\)
Suy ra \(\widehat {IMN} = 90^\circ - \widehat {MNI} = 90^\circ - 64^\circ = 26^\circ \)
Vận dụng 4
Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là ${3,2}$cm và ${2,4}$cm.


Sử dụng tính chất của hình thoi
Advertisements (Quảng cáo)

Do hai đường chéo của hình thoi vuông góc với nhau tạo thành 4 tam giác vuông bằng nhau nên áp dụng định lý Pythagore vào mỗi tam giác vuông, ta có độ dài cạnh hình vuông là:
\(\sqrt {{{\left( {\frac{{3,2}}{2}} \right)}^2} + {{\left( {\frac{{2,4}}{2}} \right)}^2}} = \sqrt 4 = 2\) (cm)
Hoạt động 6
Cho \(ABCD\) là một hình bình hành. Giải thích tại sao tứ giác \(ABCD\) có bốn cạnh bằng nhau trong mỗi trường hợp sau:
Trường hợp 1: \(AB = AD\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là phân giác góc \(BAD\)
Trường hợp 4: \(BD\) là phân giác góc \(ABC\)
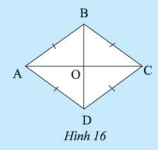

Áp dụng tính chất của hình bình hành

a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra : \(AB = CD\); \(AD = BC\) (1)
\(O\) là trung điểm của \(AC\) và \(BD\)
TH1: Nếu \(AB = AD\) suy ra \(AB = BC = CD = AD\)
TH2: \(AC\) vuông góc với \(BD\)
Suy ra bốn tam giác vuông \(OAB\), \(OAD\), \(OCD\), \(COB\) bằng nhau
Suy ra \(AB = BC = CD = DA\)
TH3: \(AC\) là phân giác của góc \(BAD\)
Suy ra \(AO\) là phân giác của góc \(BAD\)
Mà \(AO\) là trung tuyến của \(\Delta ABD\)
Suy ra \(\Delta ABD\) cân tại \(A\)
Suy ra \(AB = AD\) (3)
Từ (1), (3) suy ra \(AB = BC = CD = DA\)
TH4: Chứng minh tương tự
Vận dụng 5
Một hoa văn trang trí được ghép bởi ba hình tứ giác có độ dài mỗi cạnh đều bằng 2cm (hình 18). Gọi tên các tứ giác này và tính chu vi của hoa văn.


Áp dụng dấu hiệu nhận biết của hình thoi

Các tứ giác trên là hình thoi vì có 4 cạnh bằng nhau
Chu vi của hoa văn là: \(2 \times 4 \times 3 = 24\) (cm)
Vận dụng 6
Một tứ giác có chu vi là \(52\) cm và một đường chéo là \(24\)cm. Tính độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.

Chứng minh tứ giác là hình thoi
Tính độ dài cạnh, đường chéo

Do tứ giác có hai đường chéo vuông góc tại trung điểm của mỗi đường (gt)
Suy ra tứ giác là hình thoi
Độ dài cạnh là \(52:4 = 13\) (cm)
Do hình thoi có hai đường chéo vuông góc, tạo thành 4 tam giác vuông bằng nhau.
Độ dài nửa đường chéo còn lại là: \(\sqrt {{{13}^2} - {{\left( {24:2} \right)}^2}} = \sqrt {169 - 144} = \sqrt {25} = 5\) (cm)
Độ dài đường chéo còn lại là: \(5.2 = 10\) (cm)
