Hoạt động 4
Cho tứ giác \(ABCD\) có bốn góc bằng nhau và có bốn cạnh bằng nhau. Hãy chứng tỏ \(ABCD\) vừa là hình thoi vừa là hình thoi vừa là hình chữ nhật.
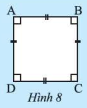

Áp dụng dấu hiệu nhận biết hình thoi và hình chữ nhật

Xét tứ giác \(ABCD\) có bốn góc bằng nhau: \(\widehat A = \widehat B = \widehat C = \widehat D\) mà \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Suy ra \(\widehat A = \widehat B = \widehat C = \widehat D = \frac{{360^\circ }}{4} = 90^\circ \)
Suy ra \(ABCD\) là hình chữ nhật
Xét tứ giác \(ABCD\) có bốn cạnh \(AB = BC = CD = DA\) nên là hình thoi
Vậy \(ABCD\) vừa là hình thoi vừa là hình chữ nhật
Hoạt động 5
Cho hình vuông \(MNPQ\). Chứng minh \(MNPQ\) vừa là hình chữ nhật vừa là hình thoi.
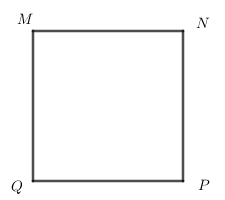

Sử dụng định nghĩa hình vuông, dấu hiệu nhận biết của hình thoi và hình chữ nhật

Vì \(MNPQ\) là hình vuông (gt)
Suy ra \(MN = NP = PQ = QM\) nên \(MNPQ\) là hình thoi
Và \(\widehat M = \widehat N = \widehat P = \widehat Q = 90^\circ \) nên \(MNPQ\) là hình chữ nhật
Vậy\(MNPQ\) vừa là hình thoi vừa là hình chữ nhật
Thực hành 3
Tìm hình vuông trong hai hình sau:
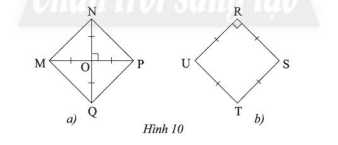

Áp dụng định nghĩa hình vuông để tìm hình vuông trong hình vẽ

a) Xét tứ giác \(MNPQ\) có hai đường chéo \(MP\) và \(NQ\) cắt nhau tại trung điểm \(O\)
Suy ra \(MNPQ\) là hình bình hành
Mà hai đường chéo \(MP\) và \(NQ\) vuông góc
Suy ra \(MNPQ\) là hình thoi
Mà \(MP = 2OM\); \(NQ = 2ON\) và \(OM = ON\) (gt)
Suy ra \(MP = NQ\)
Suy ra \(MNPQ\) là hình vuông
b) Tứ giác \(URST\) có:
\(UR = RS = ST = TU\) (gt)
Suy ra \(URST\) là hình thoi, hình bình hành
Mà \(\widehat {{\rm{UR}}S} = 90^\circ \) (gt)
Suy ra \(URST\) là hình chữ nhật
Do đó \(URST\) có 4 góc vuông
Mà \(URST\) có 4 cạnh bằng nhau
Suy ra \(URST\) là hình vuông
Vận dụng 3
Tìm bốn ví dụ về hình vuông trong thực tế

Sử dụng định nghĩa hình vuông

Mặt bàn hình vuông
Ô cửa sổ hình vuông
Hộp phấn
Viên gạch
Hoạt động 6
Cho hình chữ nhật \(ABCD\). Giải thích tại sao \(ABCD\) là hình vuông trong mỗi trường hợp sau:
Trường hợp 1: \(AB = BC\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là đường phân giác của góc \(BAD\)

Áp dụng tính chất của hình chữ nhật, định nghĩa hình vuông

\(ABCD\) là hình chữ nhật (gt)
Suy ra \(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\) (3)
\(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \) (1)
TH1:
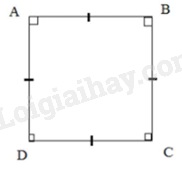
Nếu \(AB = BC\) (gt) thì \(AB = BC = CD = DA\) (2)
Từ (1), (2) suy ra \(ABCD\) là hình vuông
TH2:
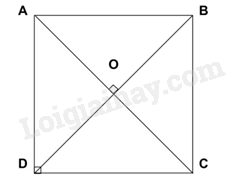
Nếu \(AC\) vuông góc với \(BD\)
Advertisements (Quảng cáo)
Mà \(ABCD\) cũng là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (4)
Từ (1) và (4) suy ra \(ABCD\) là hình vuông
TH3:
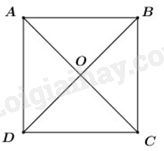
\(AC\) là phân giác của góc \(BAD\)
Mà \(ABCD\) là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (5)
Từ (1) và (5) suy ra \(ABCD\) là hình vuông
Hoạt động 7
Cho hình thoi \(ABCD\). Hãy chứng tỏ:
a) Nếu \(\widehat {BAD}\) là góc vuông thì ba góc còn lại của hình thoi cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {BAD}\) là góc vuông

Áp dụng tính chất của hình thoi, hình bình hành

a)
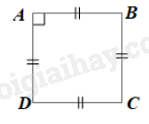
\(ABCD\) là hình thoi nên cũng là hình bình hành.
Suy ra:
\(AB = BC = CD = DA\);
\(\widehat A = \widehat C;\;\widehat B = \widehat D\)
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Suy ra: \(\widehat A + \widehat B = \widehat C + \widehat D = 180^\circ \)
Mà \(\widehat {BAD}\) là góc vuông
Suy ra \(\widehat {BCD} = 90^\circ \); \(\widehat B = 90^\circ ;\;\widehat D = 90^\circ \)
b) Nếu \(AC = BD\) thì \(ABCD\) là hình chữ nhật
Khi đó \(\widehat {BAD}\) là góc vuông
Thực hành 4
Trong Hình 12, cho biết \(ABCD\) là một hình vuông. Chứng minh rằng:
a) Tứ giác \(EFGH\) có ba góc vuông
b) \(HE = HG\)
c) Tứ giác \(EFGH\) là một hình vuông
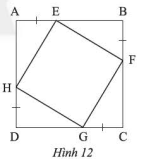

Áp dụng tính chất của hình vuông, hai tam giác bằng nhau

a) Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\); \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \)
Mà \(AE = BF = CG = HD\) (gt) suy ra \(BE = CF = DG = AH\)
Xét \(\Delta AEH\) và \(\Delta DHG\) ta có:
\(\widehat {\rm{A}} = \widehat {\rm{D}} = 90\)
\(AE = GH\) (gt)
\(AH = DG\) (gt)
Suy ra \(\Delta AEH = \Delta DHG\) (c-g-c)
Suy ra \(\widehat {{\rm{AEH}}} = \widehat {{\rm{DHG}}}\) (hai góc tương ứng)
Mà \(\widehat {AEH} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {DHG} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {EHG} = 90^\circ \)
Chứng minh tương tự ta được \(\widehat {HGF} = 90^\circ ;\;\widehat {GFE} = 90^\circ \)
Vậy tứ giác \(EFGH\) có ba góc vuông.
b) Vì \(\Delta AEH = \Delta DHG\) (cmt)
Suy ra \(HE = HG\) (2)
Từ (1) và (2) suy ra \(EFGH\) là hình vuông
c) chứng minh tương tự câu b ta có: \(HE = EF\); \(HE = FG\)
Khi đó \(EFGH\) có \(HE = HG = EF = FG\) nên là hình thoi (3)
Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (4)
Từ (3) và (4) suy ra \(EFGH\) là hình vuông
Vận dụng 4
Bạn Nam kiểm tra mặt kính của chiếc đồng hồ để bàn và nhận thấy có ba góc vuông và hai cạnh kề bằng nhau (Hình 13). Hãy cho biết mặt kính đồng hồ có hình gì?


Áp dụng dấu hiệu nhận biết của hình vuông

Mặt kính đồng hồ có ba góc vuông nên là hình chữ nhật
Mà mặt kính có hai cạnh kề bằng nhau
Suy ra mặt kính đồng hồ là hình vuông
