Luyện tập - Chủ đề 3 : Hình lăng trụ đứng - Bài tập 22 trang 112 Tài liệu dạy – học Toán 8 tập 2. Giải bài tập Cho hai tam giác cân CAF và DAF có chung đáy AF và không cùng nằm trong một mặt phẳng, cho B là trung điểm của AF. Theo em, đường thẳng AF có vuông góc cới (CBD) không ? Tại sao ?

Cho hai tam giác cân CAF và DAF có chung đáy AF và không cùng nằm trong một mặt phẳng, cho B là trung điểm của AF. Theo em, đường thẳng AF có vuông góc cới (CBD) không ? Tại sao ?
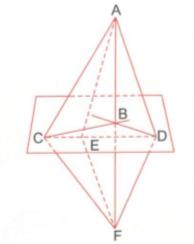

∆ACF cân tại C có CB là đường trung tuyến (B là trung điểm của AF)
Advertisements (Quảng cáo)
=> CB cũng là đường cao \( \Rightarrow CB \bot AF\)
∆ADF cân tại D có DB là đường trung tuyến (B là trung điểm của AF)
=> BD cũng là đường cao ∆ADF \( \Rightarrow BD \bot AF\)
Ta có \(AF \bot CB\) và \(AF \bot BD\) => Đường thẳng AF vuông góc với (CBD)
