
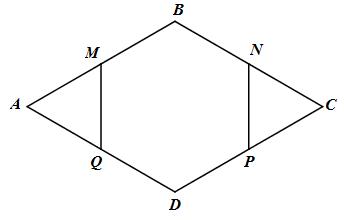
Cho hình thoi ABCD có \(\widehat B = 120^\circ \). Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác MBNPDQ là lục giác đều.

Ta có: \(\widehat A + \widehat B = {180^0}\) (hai góc trong cùng phía và AB // CD)
\( \Rightarrow \widehat A + {120^0} = {180^0} \Rightarrow \widehat A = {60^0}\)
\(\Delta ABD\) cân tại A \(\left( {AB = AD} \right)\) có \(\widehat A = {60^0}\) \( \Rightarrow \Delta ABD\) đều
M, Q lần lượt là trung điểm của AB và AD (gt)
Advertisements (Quảng cáo)
\( \Rightarrow MQ\) là đường trung bình của tam giác ABD \( \Rightarrow MQ = {1 \over 2}BD\)
N, P lần lượt là trung điểm của BC và CD (gt)
\( \Rightarrow NP\) là đường trung bình của tam giác BCD \( \Rightarrow NP = {1 \over 2}BD\)
Mà \(BD = AB\,\,(\Delta ABD\) đều) \( \Rightarrow MQ = NP = {{AB} \over 2}\)
Hình thoi ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên \(MB = BN = PD = QD = {{AB} \over 3}\)
Mặt khác \(MQ = NP = {{AB} \over 2}\). Do đó \(MB = BN = PD = QD = MQ = NP\)
\( \Rightarrow \) Đa giác MBNPDQ là lục giác đều.
