
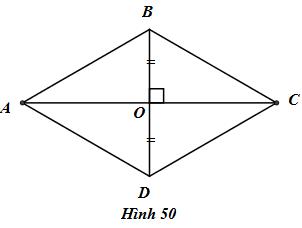
Cho hình bình hành ABCD có đường chéo AC và BD vuông góc với nhau (h.50). Hãy sắp xếp các câu theo đúng thứ tự để chứng minh ABCD là hình thoi.
a) Xét \(\Delta AOB\) và \(\Delta AOD\) có:
b) OB = OD ( tính chất đường chéo hình bình hành)
c) Suy ra \(\Delta AOB = \Delta AOD(c.g.c)\)
d) \(\widehat {AOB} = \widehat {AOD} = {90^o}(AC \bot BD)\)
e) Mà AB = CD và AD = BC (ABCD là hình bình hành)
f) OA là cạnh chung.
g) Do đó AB = AD.
h) Vậy AB = BC = CD = DA, suy ra ABCD là hình thoi.
Advertisements (Quảng cáo)

Sắp xếp:
a) Xét \(\Delta AOB\) và \(\Delta AOD\) có:
b) OB = OD ( tính chất đường chéo hình bình hành)
f) OA là cạnh chung.
d) \(\widehat {AOB} = \widehat {AOD} = {90^o}(AC \bot BD)\)
c) Suy ra \(\Delta AOB = \Delta AOD(c.g.c)\)
g) Do đó AB = AD.
e) Mà AB = CD và AD = BC (ABCD là hình bình hành)
h) Vậy AB = BC = CD = DA, suy ra ABCD là hình thoi.
