
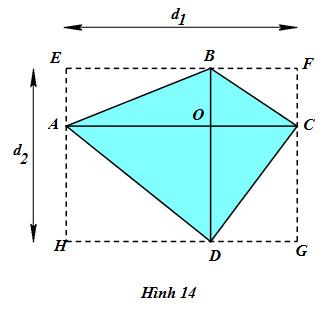
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau và có độ dài lần lượt là AC = d1, BD = d2 (h.14). Hãy chứng tỏ hình chữ nhật EFGH có diện tích gấp đôi tứ giác ABCD. Từ đó, diện tích tứ giác ABCD.

\({S_{EBOA}} = OA.OB\) (EBOA là hình chữ nhật),
\({S_{OAB}} = {1 \over 2}OA.OB\) (\(\Delta OAB\) vuông tại O)
Do đó \({S_{EBOA}} = 2{S_{OAB}}\)
Advertisements (Quảng cáo)
Tương tự: \({S_{BFCO}} = 2{S_{OBC}},\,\,{S_{OCGD}} = 2{S_{OCD}},\,\,{S_{AODH}} = {S_{OAD}}\)
Do vậy
\(\eqalign{ & {S_{EFGH}} = {S_{EBOA}} + {S_{BFCO}} + {S_{OCGD}} + {S_{AODH}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 2{S_{OAB}} + 2{S_{OBC}} + 2{S_{OCD}} + 2{S_{OAD}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 2\left( {{S_{OAB}} + {S_{OBC}} + {S_{OCD}} + {S_{OAD}}} \right) = 2{S_{ABCD}} \cr} \)
Mà \({S_{EFGH}} = {d_1}{d_2}\)
Do đó \(2{S_{ABCD}} = {d_1}{d_2}\).
Vậy \({S_{ABCD}} = {1 \over 2}{d_1}{d_2}\).
