Advertisements (Quảng cáo)
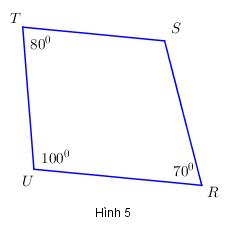
1. Tìm số đo góc S ở hình 5:
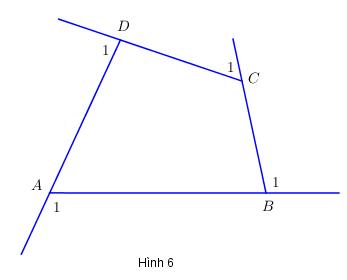
2. Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác. Hãy tính tổng bốn góc ngoài \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\) của tứ giác ABCD ở hình 6.
1. Tứ giác TSRU có: \(\widehat T + \widehat S + \widehat R + \widehat U = {360^0}\)
Mà \(\widehat T = {80^0};\,\,\widehat R = {70^0};\,\,\widehat U = {100^0}\)
Advertisements (Quảng cáo)
Do đó \({80^0} + \widehat S + {70^0} + {100^0} = {360^0} \Leftrightarrow {250^0} + \widehat S = {360^0} \Leftrightarrow \widehat S = {360^0} – {250^0} = {110^0}\)
2. Ta có: \(\widehat A + \widehat {{A_1}} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {{A_1}} = {180^0} – \widehat A\)
Tương tự \(\widehat {{B_1}} = {180^0} – \widehat B;\,\,\widehat {{C_1}} = {180^0} – \widehat C;\,\,\widehat {{D_1}} = {180^0} – \widehat D\)
Tứ giác ABCD có \(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\)
Do đó
\(\eqalign{ & \widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = \left( {{{180}^0} – \widehat A} \right) + \left( {{{180}^0} – \widehat B} \right) + \left( {{{180}^0} – \widehat C} \right) + \left( {{{180}^0} – \widehat D} \right) \cr & = {720^0} – \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right) = {720^0} – {360^0} = {360^0} \cr} \)