Bài 35 Chứng minh rằng nếu tam giác A\'B\'C\' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng K. Bài 35 trang 79 - Sách giáo khoa toán 8 tập 2 - Trường hợp đồng dạng thứ ba
Bài 35 Chứng minh rằng nếu tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng K.

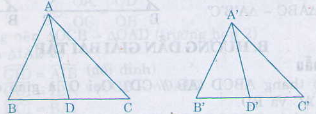
Xét ∆A’B’D’ và ∆ABD có:
\(\widehat{B}\) = \(\widehat{B'}\)
Advertisements (Quảng cáo)
\(\widehat{BAD}\) = \(\widehat{B'A'D'}\)
=> ∆’B’D’ ∽ ∆ABD theo tỉ số K = \(\frac{A'B'}{AB}\)= \(\frac{A'D'}{AD}\)
Mà ∆A’B’C’ ∽ ∆ABC theo tỉ số = \(\frac{A'B'}{AB}\)
=> \(\frac{A'D'}{AD}\) = k
