Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF.. Bài 44 trang 92 sgk toán 8 tập 1 - Hình bình hành
Bài 44. Cho hình bình hành \(ABCD\). Gọi \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\). Chứng minh rằng \(BE = DF\).

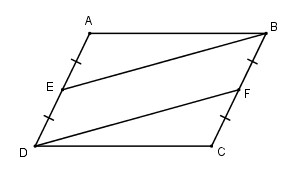
Tứ giác \(BEDF\) có:
\(DE // BF\) và \(AD=BC\) ( vì \(ABCD\) hình bình hành)
Advertisements (Quảng cáo)
\(E\) là trung điểm của \(AD\) nên \(DE = \frac{1}{2}AD\)
\(F\) là trung điểm của \(BC\) nên \(BF= \frac{1}{2}BC\)
Mà \(AD=BC\) nên \(DE=BF\)
Tứ giác \(BEDF\) có \(DE//BF\) và \(DE=BF\) nên \(BEDF\) là hình bình hành (theo dấu hiệu nhận biết hình bình hành).
Suy ra \(BE = DF\). (tính chất hình bình hành)
