Bài 47. Cho hình 72, trong đó \(ABCD\) là hình bình hành.
a) Chứng minh rằng \(AHCK\) là hình bình hành.
b) Gọi \(O\) là trung điểm của \(HK\). Chứng minh rằng ba điểm \(A, O, C\) thẳng hàng
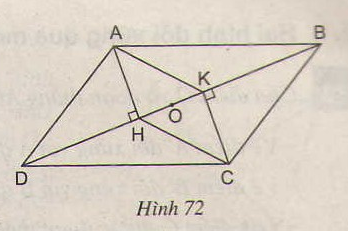

a) Xét hai tam giác vuông \(AHD\) và \(CKB\) có:
\( AD = CB\) (vì \(ABCD\) là hình bình hành)
Advertisements (Quảng cáo)
\(\widehat {ADH} = \widehat {CBK}\) (hai góc ở vị trí so le trong)
Suy ra \(∆AHD = ∆CKB\) (cạnh huyền- góc nhọn)
Suy ra \(AH = CK\)
\(AH\bot BD\) và \(CK\bot BD\) suy ra \(AH//CK\)
Tứ giác \(AHCK\) có \(AH//CK\) và \(AH = CK\) nên là hình bình hành (theo dấu hiệu nhận biết hình bình hành),
b) Xét hình bình hành \(AHCK\) có \(O\) là trung điểm của \(HK\), do đó \(O\) là giao điểm của hai đường chéo \(AC\) và \(HK\) của hình bình hành.
Hay \(A,O,C\) thẳng hàng
