Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
a)Chứng minh rằng điểm E đối xứng với điểm M qua AB.
b)Các tứ giác AEMC, AEBM là hình gì? Vì sao?
c)Cho BC = 4cm, tính chu vi tứ giác AEBM.
d)Tam giác vuông ABC, có điều kiện gì thì AEBM là hình vuông?
Hướng dẫn làm bài:
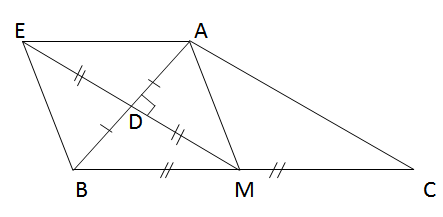
a)Ta có MB = MC, BD = DA
nên MD là đường trung bình của ∆ABC
Do đó MD // AC
Do AC ⊥ AB nên MD ⊥ AB
Ta có AB là đường trung trực của ME (do AB ⊥ ME tại D và DE = DM) nên E đối xứng với M qua AB.
b)+Ta có: EM // AC (do MD // AC)
EM = AC (cùng bằng 2DM)
Advertisements (Quảng cáo)
Nên AEM (là hình bình hành)
+Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c)Ta có BC = 4 cm =>BM = 2 cm.
Chu vi hình thoi AEBM bằng 4.BM = 4. 2 = 8(cm)
d)Cách 1 :
Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức là tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
Cách 2 :
Hình thoi AEBM là hình vuông ⇔AM ⊥ BM
⇔ABC có trung tuyến AM là đường cao
⇔∆ABC cân tại A.
Vậy nếu ∆ABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.
