Trả lời câu hỏi 3 Bài 9 trang 98 Toán 8 Tập 1 . c) Định lí: Trong một tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.. Bài 9. Hình chữ nhật
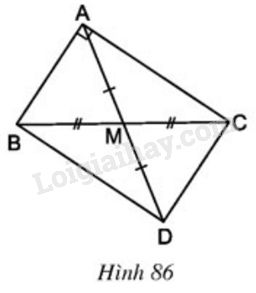
Cho hình \(86\):
a) Tứ giác \(ABDC\) là hình gì? Vì sao?
b) So sánh các độ dài \(AM\) và \(BC.\)
c) Tam giác vuông \(ABC\) có \(AM\) là đường trung tuyến ứng với cạnh huyền. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lí.
Áp dụng:
- Dấu hiệu nhận biết hình bình hành.
Advertisements (Quảng cáo)
- Dấu hiệu nhận biết hình chữ nhật.
a) Tứ giác \(ABDC\) có hai đường chéo cắt nhau tại trung điểm mỗi đường \(⇒ ABDC\) là hình bình hành.
Hình bình hành \(ABDC\) có góc \(A\) vuông \(⇒ ABDC\) là hình chữ nhật.
b) Hình chữ nhật \(ABDC ⇒ AD = BC\) (hai đường chéo bằng nhau).
\(\dfrac{{AD}}{2} = \dfrac{{BC}}{2} \Rightarrow AM = \dfrac{{BC}}{2}\)
c) Định lí: Trong một tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.