
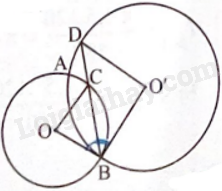
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B phân biệt. Đường phân giác của \(\widehat {OBO’}\) cắt các đường tròn (O), (O’) tại các điểm thứ hai theo thứ tự là C và D. So sánh \(\widehat {BOC}\) và \(\widehat {BO’D}\).

Chứng minh \(\widehat {OBC} = \widehat {OCB} = \widehat {CBO’} = \widehat {O’DB}\) sau đó so sánh \(\widehat {BOC}\) và \(\widehat {BO’D}\).

Advertisements (Quảng cáo)
Ta có \(\widehat {OBC} = \widehat {CBO’}\) (vì BC là đường phân giác của \(\widehat {OBO’}\)).
Ta lại có \(\widehat {OBC} = \widehat {OCB}\) (vì tam giác OBC cân tại O),
\(\widehat {CBO’} = \widehat {O’DB}\) (vì tam giác O’BD cân tại O’).
Suy ra \(\widehat {OBC} = \widehat {OCB} = \widehat {CBO’} = \widehat {O’DB}\),
\(\widehat {BOC} = \widehat {BO’D}\).
