
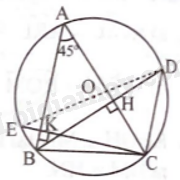
Cho tam giác nhọn ABC có \(\widehat {BAC} = {45^o}\) và có các đỉnh nằm trên đường tròn (O). Các đường cao BH, CK cắt đường tròn (O) tại D, E. Chứng minh ba điểm D, O, E thẳng hàng.

Dựa vào các góc nội tiếp cùng chắn một cung thì bằng nhau để chứng minh DE là đường kính.

Advertisements (Quảng cáo)
Ta có \(BH \bot AC\) nên tam giác ABH vuông tại H. Mà \(\widehat {BAH} = {45^o}\) nên \(\widehat {ABH} = {45^o}\).
Mặt khác \(\widehat {ABD} = \widehat {ACD}\) (góc nội tiếp cùng chắn \(\overset\frown{AD}\)) nên \(\widehat {ACD} = {45^o}\) (1)
Ta có \(CK \bot AB\) nên tam giác ACK vuông tại K. Mà \(\widehat {CAK} = {45^o}\) nên \(\widehat {ACK} = {45^o}\) (2)
Từ (1) và (2) suy ra \(\widehat {DCE} = {90^o}\) nên DE là đường kính.
Vậy ba điểm D, O, E thẳng hàng.
