
Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, \(MN = n\) (mét), \(MP = p\) (mét), \(p > n\) và \(\widehat {MPA} = \alpha \) (H.4.12). Chứng minh rằng: \(AB = \frac{{p\tan \alpha - n}}{{\sin \alpha }}\).
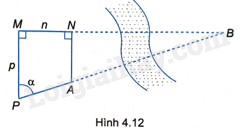

+ Chứng minh \(\widehat {BAN} = \widehat {BPM} = \alpha \).
+ Tam giác BAN vuông tại N có: \(BN = AB.\sin \alpha \).
+ Tam giác BPM vuông tại M có: \(BM = PM\tan \alpha = p\tan \alpha \).
+ \(BM - BN = MN = n\) nên \(p\tan \alpha - AB\sin \alpha = n\), từ đó tính được AB theo n, p, \(\alpha \).

Advertisements (Quảng cáo)
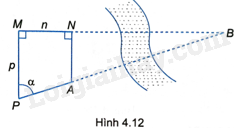
Vì AN//PM nên \(\widehat {BAN} = \widehat {BPM} = \alpha \).
Tam giác BAN vuông tại N có:
\(BN = AB.\sin \alpha \).
Tam giác BPM vuông tại M có:
\(BM = PM\tan \alpha = p\tan \alpha \).
Vì \(BM - BN = MN = n\) nên \(p\tan \alpha - AB\sin \alpha = n\).
Suy ra \(AB = \frac{{p\tan \alpha - n}}{{\sin \alpha }}\).
