
Xét điểm B nằm giữa hai điểm A và H. Giả sử có điểm D sao cho DH vuông góc với AB và \(\widehat {DAH} = {15^o},\widehat {DBH} = {30^o}\). Chứng minh rằng \(HD = \frac{{AB}}{2}\).

+ Tam giác HDB vuông tại H nên \(\frac{{HD}}{{BD}} = \sin \widehat {HBD}\).
+ Tính được góc ADB của tam giác ABD, từ đó suy ra tam giác ABD cân tại D nên \(BD = AB\).
+ Do đó, \(BD = AB = 2HD\), suy ra điều phải chứng minh.
Advertisements (Quảng cáo)

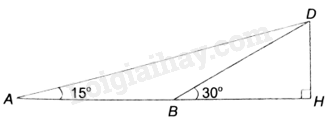
Tam giác HDB vuông tại H nên \(\frac{{HD}}{{BD}} = \sin \widehat {HBD} = \sin {30^o} = \frac{1}{2}\) nên \(BD = 2HD\).
Tam giác ABD có \(\widehat {ABD} = {180^o} - \widehat {DBH} = {150^o},\) \(\widehat {BAD} = {15^o}\) nên \(\widehat {ADB} = {180^o} - \widehat {ABD} - \widehat A = {15^o}\).
Do đó tam giác ABD cân tại B. Suy ra \(BD = AB\).
Suy ra \(BD = AB = 2HD\) nên \(HD = \frac{{AB}}{2}\).
