Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối. Lời Giải - Bài 4.30 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 1 - Chương IV. Hệ thức lượng trong tam giác vuông. Cho hai tòa nhà cách nhau 32m. Tại điểm A trên nóc tòa nhà cao nhìn xuống nóc D và chân C của tòa nhà thấp lần lượt theo các góc ({15^o}) và ({43^o}) (so với phương nằm ngang) (H. 4. 16)...

Cho hai tòa nhà cách nhau 32m. Tại điểm A trên nóc tòa nhà cao nhìn xuống nóc D và chân C của tòa nhà thấp lần lượt theo các góc \({15^o}\) và \({43^o}\) (so với phương nằm ngang) (H.4.16). Tính chiều cao của hai tòa nhà đó (làm tròn đến m).
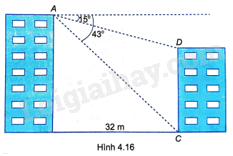

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối.

Advertisements (Quảng cáo)
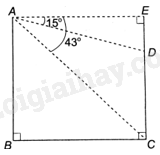
Gọi B là chân tòa nhà cao.
Tam giác ABC vuông tại B nên \(AB = BC.\tan \widehat {ACB} = 32.\tan {43^o} \approx 30\left( m \right)\)
Tam giác ADE vuông tại E nên \(ED = AE.\tan \widehat {EAD} = 32.\tan {15^o} \approx 9\left( m \right)\)
Do đó, tòa nhà cao tầng có chiều cao \(BA \approx 30m\) và tòa nhà thấp hơn có chiều cao \(CD = CE - ED = AB - ED \approx 21m\)
