
Xét tam giác ABC vuông tại B, có \(\widehat A = {30^o}\). Tia Bt sao cho \(\widehat {CBt} = {30^o}\) cắt tia AC ở D, D nằm giữa A và C. Chứng minh rằng khoảng cách từ D đến đường thẳng BC bằng \(\frac{{AB}}{4}\).

+ Tam giác ABC vuông tại B, \(\widehat A = {30^o}\) nên tính được góc C.
+ Tính góc BDC từ đó suy ra tam giác BDC vuông tại D, suy ra \(\frac{{BD}}{{AB}} = \sin \widehat {BAD}\).
+ Gọi E là chân đường vuông góc kẻ từ D lên BC thì DE là khoảng cách từ D đến đường thẳng BC.
+ Tam giác BDE vuông tại E nên \(\frac{{DE}}{{BD}} = \sin \widehat {DBE}\).
+ Ta có: \(\frac{{DE}}{{AB}} = \frac{{DE}}{{BD}}.\frac{{BD}}{{AB}}\), từ đó tính được \(DE = \frac{{AB}}{4}\).
Advertisements (Quảng cáo)

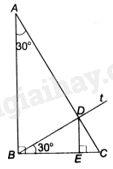
Tam giác ABC vuông tại B nên \(\widehat C = {90^o} - \widehat A = {60^o}\).
Tam giác BCD có: \(\widehat {BDC} = {180^o} - \widehat {DBC} - \widehat C = {90^o}\). Do đó, tam giác BCD vuông tại D.
Suy ra, \(\frac{{BD}}{{AB}} = \sin \widehat {BAD} = \sin {30^o} = \frac{1}{2}\)
Gọi E là chân đường vuông góc kẻ từ D lên BC thì DE là khoảng cách từ D đến đường thẳng BC.
Trong tam giác BDE vuông tại E có: \(\frac{{DE}}{{BD}} = \sin \widehat {DBE} = \sin {30^o} = \frac{1}{2}\)
Ta có: \(\frac{{DE}}{{AB}} = \frac{{DE}}{{BD}}.\frac{{BD}}{{AB}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4}\), suy ra \(DE = \frac{{AB}}{4}\).
